Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo
En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:
También puede escribir el Schr # 246-dinger ecuación de esta manera, donde H es el operador hamiltoniano hermítica:
Eso es en realidad el independiente del tiempo Schr # ecuación 246-dinger. El Schr # 246-dinger ecuación dependiente del tiempo se ve así:
La combinación de las tres ecuaciones anteriores le da la siguiente, que es otra forma de la Schr # 246-dinger ecuación dependiente del tiempo:
Y debido a que está tratando con una sola dimensión, X, esta ecuación se convierte en
Esto es más sencillo de lo que parece, sin embargo, porque el potencial no cambia con el tiempo. De hecho, debido E es constante, puede volver a escribir la ecuación como
Esa ecuación hace la vida mucho más simple - es fácil de resolver el Schr # 246-dinger ecuación dependiente del tiempo, si usted está tratando con un potencial constante. En este caso, la solución es
Ordenado. Cuando el potencial no varía con el tiempo, la solución a la Schr # 246-dinger ecuación dependiente del tiempo se convierte simplemente en
la parte espacial, multiplicado por
la parte dependiente del tiempo.
Así que cuando se agrega en la parte dependiente del tiempo de la función de onda independiente del tiempo, se obtiene la función de onda dependiente del tiempo, que se ve así:
La energía de la nestado cuántico XX es
Por lo tanto, el resultado es
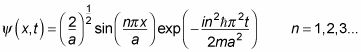
donde exp (X) = eX.
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno -
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…
Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que…
La teoría de cuerdas: la función de onda cuántica La solución al problema del experimento rendija doble, un concepto en el corazón de los orígenes de la teoría de cuerdas y una consecuencia directa de este primer trabajo en la física cuántica, tomó la forma de la función de onda cuántica,…