Aplicando la ecuación schr & # 246-dinger en tres dimensiones
En la física cuántica, se puede aplicar el Schr # 246-dinger ecuación cuando se trabaja en los problemas que tienen un potencial central. Estos son problemas donde usted es capaz de separar la función de onda en una parte radial (que depende de la forma del potencial) y una parte angular, que es un armónico esférico.
Potenciales centrales son esféricamente simétricas potenciales, de la clase donde V (r) = V (r). En otras palabras, el potencial es independiente de la naturaleza del vector del radio vector del potencial depende sólo la magnitud del vector r (cual es r), No en el ángulo de r.
El Schr # 246-dinger ecuación tiene este aspecto en tres dimensiones, donde
es el operador de Laplace:
Y el operador Laplaciano tiene este aspecto en coordenadas rectangulares:
En coordenadas esféricas, que es un poco complicado, pero se puede simplificar más tarde. Echa un vistazo a el operador Laplaciano esférica:
Aquí, L2 es el cuadrado del momento angular orbital:
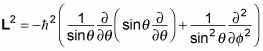
Así que en coordenadas esféricas, la Schr # 246-dinger ecuación para un potencial centro tiene este aspecto cuando se sustituye en los términos:
Echa un vistazo a la ecuación anterior. El primer término corresponde efectivamente a la energía cinética radial - es decir, la energía cinética de la partícula que se mueve en la dirección radial. El segundo término corresponde al la energía cinética de rotación. Y el tercer término corresponde al energía potencial.
Entonces, ¿qué se puede decir de las soluciones a esta versión de la Schr # 246-dinger ecuación? Usted puede notar que el primer término depende sólo r, al igual que el tercero, y que el segundo término depende sólo de los ángulos. Así que usted puede romper la función de onda,
en dos partes:
Una parte radial
Una parte que depende de los ángulos
Esta es una propiedad especial de los problemas con los potenciales centrales.
-
Aplicando la ecuación radial fuera de la plaza, así -
Aplicando la ecuación radial en el interior del pozo cuadrado -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de la parte angular de una función de onda -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…
Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que…