Cómo desvincular diferentes partículas en ecuaciones linealmente independientes

En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un sistema de muchos tipos diferentes de coches flotando en el espacio. Usted puede distinguir todos esos coches porque son todos diferentes - tienen diferentes masas, por una cosa.

Ahora decir que cada vehículo interactúa con su propio potencial - es decir, el potencial de que cualquier coche ve no depende de cualquier otro coche. Eso significa que el potencial de todos los coches es sólo la suma de los potenciales individuales cada vehículo ve, lo que se parece a esto, suponiendo que tiene vehículos N:

Ser capaz de cortar la energía potencial hasta en una suma de términos independientes como éste hace la vida mucho más fácil. Esto es lo que el hamiltoniano se ve así:

Observe cómo mucho más simple de esta ecuación es que esto de Hamilton para el átomo de hidrógeno:

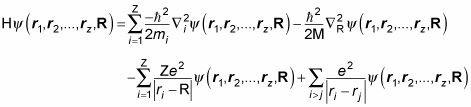
Observe que puede separar la ecuación anterior para el potencial de todos los coches en n diferentes ecuaciones:

Y la energía total es la suma de las energías de los coches individuales:

Y la función de onda es simplemente el producto de las funciones de onda individuales:

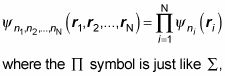
excepto que significa un producto de términos, no una suma, y n_yo se refiere a todos los números cuánticos del yoº partícula.

Como puede ver, cuando las partículas que está trabajando son distinguibles y con sujeción a los potenciales independientes, el problema del manejo de muchos de ellos se hace más simple. Usted puede romper el sistema para arriba en sistemas de una sola partícula independientes N. La energía total es la suma de las energías individuales de cada partícula. El Schr # 246-dinger ecuación se divide en N diferentes ecuaciones. Y la función de onda termina simplemente ser el producto de las funciones de onda de las partículas de diferentes N.

Echa un vistazo a un ejemplo. Digamos que tienes cuatro partículas, cada una con una masa diferente, en una plaza bien. Usted quiere encontrar la energía y la función de onda de este sistema. Esto es lo que el potencial del pozo cuadrado tiene este aspecto para cada una de las cuatro partículas no interactúan:

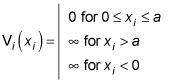
Aquí está lo que el Schr # 246-dinger ecuación es así:

Puede separar la ecuación anterior en cuatro ecuaciones de una sola partícula:

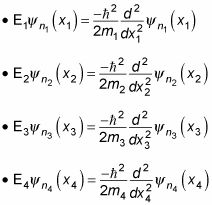
Los niveles de energía son

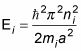
Y debido a que la energía total es la suma de las energías individuales es

la energía es en general

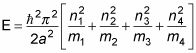
Así que aquí está la energía del estado fundamental - donde todas las partículas están en sus estados fundamentales, n₁ = n₂ = n₃ = n₄ = 1:

Para un sistema unidimensional con una partícula en un pozo cuadrado, la función de onda es

La función de onda para el sistema de cuatro partícula es sólo el producto de las funciones de onda individuales, por lo que se ve así:

Por ejemplo, para el estado fundamental, n₁ = n₂ = n₃ = n₄ = 1, usted tiene

Así como usted puede ver, los sistemas de N partículas independientes, distinguibles suelen ser susceptibles a la solución - todo lo que tienes que hacer es separarlos en N ecuaciones independientes.