Cómo obtener las funciones de onda incidente y dispersos de partículas spinless
Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las partículas depende sólo de su distancia relativa, |r
1 - r2|.Usted puede reducir los problemas de este tipo a dos problemas desacoplados. La primera ecuación desacoplado trata el centro de masa de las dos partículas como una partícula libre, y la segunda ecuación es para una partícula eficaz de masa
La primera ecuación desacoplado, la ecuación de libre de partículas del centro de masa, no es de interés a usted en la dispersión de las discusiones. La segunda ecuación es la de concentrarse en donde
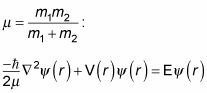
Usted puede utilizar la ecuación anterior para resolver la probabilidad de que una partícula se encuentra dispersa en un ángulo sólido
y le dará esta probabilidad por la sección transversal diferencial,
En la física cuántica, paquetes de ondas representan partículas. En términos de dispersión, estos paquetes de ondas deben ser lo suficientemente amplia como para que la difusión que se produce durante el proceso de dispersión es insignificante (sin embargo, el paquete de ondas no puede ser tan extendido que abarca todo el laboratorio, incluyendo los detectores de partículas). Aquí está el quid: Después de la dispersión, la función de onda se divide en dos partes - una parte no dispersada y una parte dispersa. Así es como la dispersión de las obras en el mundo de la física cuántica.
Derivación de la función de onda incidente
Supongamos que el potencial de dispersión V (r) Tiene un rango muy finito, la. Fuera de ese rango, las funciones de onda involucradas actúan como partículas libres. Así función de onda de la partícula incidente, fuera del límite de la V (r) - Es decir, fuera del rango la de la otra partícula - está dada por esta ecuación, ya que V (r) Es cero:
dónde
La forma
es la ecuación para una onda plana, por lo
donde A es una constante y
es el producto escalar entre el vector y la onda de la onda incidente r. En otras palabras, se está tratando la partícula incidente como una partícula de impulso
Derivación de la función de onda dispersada
Después de la dispersión de las partículas spinless, la función de onda nonscattered no es de mucho interés para usted, pero la función de onda dispersada es. Aunque la función de onda incidente tiene la forma
la función de onda dispersada tiene una forma ligeramente diferente:
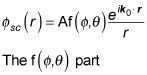
se llama la amplitud de dispersión, y su trabajo es encontrarlo. Aquí, A es un factor de normalización y
donde E es la energía de la partícula dispersa.
-
Aplicando la ecuación radial fuera de la plaza, así -
Crear funciones de onda simétricas y antisimétricos por unos sistemas de tres o más de partículas -
Crear funciones de onda simétricas y antisimétricas para un sistema de dos partículas -
Crear funciones de onda simétricas y antisimétricos para cualquier sistema de partículas n -
La determinación de la parte radial de una función de onda -
Encontrar los límites de rho pequeños y grandes de una partícula libre
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer a encontrar la ecuación de energía total para los problemas de partículas libres tridimensionales. La energía total de la partícula libre es la suma de la energía en tres…
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo el efecto Compton de la luz explica desplazamiento de longitud de onda Aunque Max Planck y Albert Einstein postuló que la luz podía comportarse como tanto una onda y una partícula, fue Arthur Compton quien finalmente demostró que esto era posible. Su experimento involucró esparciendo fotones de electrones, como la…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
¿Cómo encontrar la energía total de un sistema de múltiples partículas El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número…
Cómo normalizar la función de onda en un potencial cuadro En el curso de física cuántica, se le puede pedir a normalizar la función de onda en un potencial cuadro. He aquí un ejemplo: considere la función de ondaen el X dimensión, tiene esto para la ecuación de onda:Así que la función de onda es…
Cómo relacionar la amplitud de dispersión y la sección transversal diferencial de partículas spinless La amplitud de dispersión de partículas spinless es crucial para la comprensión de dispersión desde el punto de vista de la física cuántica. Para ver esto, eche un vistazo a las densidades de corriente, Jinc (la densidad de flujo de una…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…