¿Cómo encontrar la energía total de un sistema de múltiples partículas
El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número de partículas se identifican por su posición (ignorando spin).
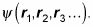
Para encontrar la energía total para este sistema, comience a trabajar con la función de onda. El estado de un sistema con muchas partículas, como se muestra en la figura, está dada por
Y aquí está la probabilidad de que la partícula 1 se encuentra en d3r1, 2 de partícula está en d3r2, partícula 3 está en d3r3, etcétera:
La normalización de las
exigencias que
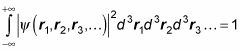
Bien, así que ¿qué pasa con el hamiltoniano, que le da a los estados de energía? Es decir, lo que es H, donde
Cuando usted está tratando con una sola partícula, puede escribir esto como
Pero en un sistema de muchas partículas hamiltoniano debe representar la energía total de todas las partículas, no sólo uno.
La energía total del sistema es la suma de la energía de todas las partículas, así que aquí está cómo se puede generalizar el hamiltoniano para sistemas multi-partículas sin centrifugado:
Esto, a su vez, es igual a lo siguiente:
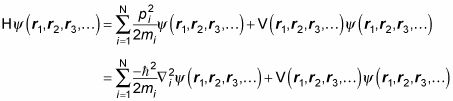
Aquí, myo es la masa de la yoTH partículas y V es el potencial multi-partícula.
-
Crear funciones de onda simétricas y antisimétricos por unos sistemas de tres o más de partículas -
Crear funciones de onda simétricas y antisimétricas para un sistema de dos partículas -
La determinación de los niveles de energía de una partícula en un potencial cuadro -
Los fermiones y bosones -
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones -
Cómo partículas túnel a través de barreras potenciales que tienen una mayor energía
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
¿Cómo distinguir partículas en un sistema multi-partícula Mecánica cuántica, las partículas idénticas en un sistema de múltiples partículas no lo conservan su individualidad en términos de cualquier, cantidad observable medible. Se pierde la individualidad de partículas idénticas tan pronto como…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica y el hamiltoniano Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
La teoría de cuerdas y el electromagnetismo: ondas de energía super-rápidos Descubierto en el siglo 19, la fuerza electromagnética (o electromagnetismo) Es una unificación de la fuerza electrostática y la fuerza magnética. En la mitad del siglo 20, esta fuerza se explicó en un marco de la mecánica cuántica llamada…
La teoría de cuerdas y partículas sin masa Un efecto secundario de la creación de una teoría de cuerdas consistente es que tuvo que contener ciertos objetos que no pueden ser llevados a descansar. Debido a que la masa es una medida de un objeto mientras se está en reposo, este tipo de…
La teoría de cuerdas y la supersimetría De acuerdo con la teoría de cuerdas, todas las partículas del universo se pueden dividir en dos tipos: bosones y fermiones. La teoría de cuerdas predice que un tipo de conexión, llamado supersimetría, existe entre estos dos tipos de…
La teoría de cuerdas: partículas de p-branas A mediados de la década de 1990, Andrew Strominger trabajo realizado en otro tipo de membrana, llamada p-branas, que eran las soluciones a las ecuaciones de campo de Einstein de la relatividad general. los p representa el número de dimensiones,…
La teoría de cuerdas: la supersimetría hipótesis supercompañeros Bajo la supersimetría, los bosones y fermiones correspondientes se llaman supercompañeros. El supercompañero de una partícula estándar se denomina una spartícula.Debido a que ninguna de las partículas existentes son supercompañeros, esto…