La medición de la energía de las partículas consolidadas y no consolidadas

En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.

Echa un vistazo a el potencial en la siguiente figura. La inmersión, o bien, en el potencial, significa que las partículas pueden ser atrapados en ella, si no tienen demasiada energía.

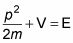
La energía cinética de la partícula suma con su energía potencial es una constante, igual a su energía total:

Si su energía total es menor que V₁, la partícula será atrapado en el pozo de potencial, como se ve en la figura- para salir del pozo, la energía cinética de la partícula tendría que ser negativa para satisfacer la ecuación, lo cual es imposible de acuerdo a la mecánica clásica.

-Mecánica cuántica hablando, hay dos estados posibles que una partícula de energía E puede tomar en el potencial dado por la figura - unido y no unido.

Estados ligados ocurren cuando la partícula no es libre de viajar al infinito - es tan simple como eso. En otras palabras, la partícula se limita a la pozo de potencial.

Una partícula que viaja en el pozo de potencial que se ve en la figura está obligado si su energía, E, está a menos de dos V₁ y V₂. En ese caso, la partícula se mueve entre X₁ y X₂. Es posible descubrir la partícula fuera de esta región.

Una partícula atrapada en un pozo como se representa por una función de onda, y se puede resolver el Schr # 246-dinger ecuación para las funciones de onda permitidas y los estados de energía permitidos. Es necesario utilizar dos condiciones de frontera (el Schr # 246-dinger ecuación es una ecuación diferencial de segundo orden) para resolver el problema por completo.

Estados consolidados son discretos - es decir, forman un espectro de energía de los niveles de energía discretos. La ecuación # 246-dinger Schr le da esos estados. Además, en problemas unidimensionales, los niveles de energía de un estado ligado no se degeneran - es decir, no hay dos niveles de energía son los mismos en todo el espectro de energía.

Si la energía de una partícula, E, es mayor que el potencial (V₁ en la figura), la partícula puede escapar de la pozo de potencial. Hay dos casos posibles: V₁ lt; E lt; V₂ y E> V₂.

Caso 1: Las partículas con energía entre los dos potenciales (V₁ lt; E lt; V₂)

Si V₁ lt; E lt; V₂, la partícula en el pozo de potencial tiene suficiente energía para superar la barrera de la izquierda, pero no a la derecha. La partícula es libre de moverse hasta el infinito negativo, por lo que su clásicamente permitida X región es entre

Aquí, los valores de energía permitidos son continuas, no discreta, porque la partícula no está completamente unido. Los valores propios de la energía no se degeneran - es decir, no hay dos valores propios de la energía son lo mismo.

El Schr # 246-dinger ecuación,

es una ecuación diferencial de segundo orden, por lo que cuenta con dos soluciones-linealmente independientes sin embargo, en este caso, sólo una de esas soluciones es física y no divergen.

La ecuación de onda en este caso resulta a oscilar de X lt; X₂ y a decaer rápidamente para X > X₂.

Caso 2: Las partículas con energía mayor que el mayor potencial (E> V₂)

Si E> V₂, la partícula no está vinculado en absoluto y es libre de viajar desde menos infinito hasta el infinito positivo.

El espectro de energía es continuo y la función de onda resulta ser una suma de una onda en movimiento a la derecha y el otro se mueve hacia la izquierda. Los niveles de energía del espectro permitido por lo tanto doblemente degenerado.