¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres
Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:
Digamos que usted está tratando con una partícula libre cuya generales potencial, V (X) = 0. En ese caso, usted tendría la siguiente ecuación:
Y usted puede reescribir esto como
donde el número de onda, k, es
Usted puede escribir la solución general a este Schr # 246-dinger ecuación como
Si agrega dependencia temporal de la ecuación, se obtiene esta función de onda dependiente del tiempo:
Eso es una solución a la Schr # 246-dinger ecuación, pero resulta ser no físico. Para ver esto, tenga en cuenta que para cualquiera de los términos de la ecuación, no se puede normalizar la densidad de probabilidad,
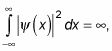
siempre que A y B no son ambos iguales a cero.
¿Que esta pasando aqui? La densidad de probabilidad para la posición de la partícula es uniforme a través de todo X! En otras palabras, no se puede precisar la partícula en absoluto.
Este es un resultado de la forma de la función de onda dependiente del tiempo, que utiliza un valor exacto para el número de onda,
Así que lo que la ecuación dice es que usted sabe E y p exactamente. Y si usted sabe p y E exactamente, lo que provoca una gran incertidumbre en X y t - De hecho, X y t son completamente incierto. Eso no se corresponde con la realidad física.
Por lo demás, la función de onda
Marylouise, puede formatear el EQ anterior como un gif? Gracias, Alexa.
tal como está, no es algo que se pueda normalizar. Tratando de normalizar el primer término, por ejemplo, le da esta integral:
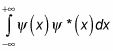
EQ tiene que ser un gif.
Recuerde que el símbolo de asterisco (*) significa el complejo conjugado. Un conjugado complejo voltea el signo que conecta las partes real e imaginaria de un número complejo.
Y para el primer período de
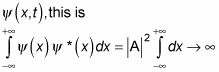
EQ tiene que ser un gif.
Y lo mismo ocurre con el segundo término de
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno -
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
Cómo relacionar la amplitud de dispersión y la sección transversal diferencial de partículas spinless La amplitud de dispersión de partículas spinless es crucial para la comprensión de dispersión desde el punto de vista de la física cuántica. Para ver esto, eche un vistazo a las densidades de corriente, Jinc (la densidad de flujo de una…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…
Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que…