Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas
Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de onda en conjunto para que usted obtenga un paquete de ondas, que es una colección de funciones de onda de la forma
de tal manera que las funciones de onda interfieren constructivamente en una ubicación y interfieren destructivamente (ir a cero) en todos los demás lugares:
Esto se suele escribir como una integral continua:
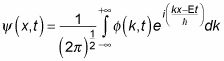
Que es
Es la amplitud de cada función de onda de componentes, y se puede encontrar
a partir de la transformada de Fourier de la ecuación:
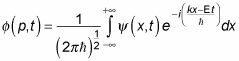
Porque
usted también puede escribir las ecuaciones de paquetes de onda de este tipo, en términos de p, no k:
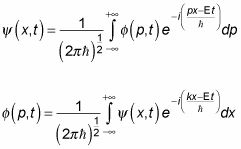
Bueno, usted puede preguntarse exactamente lo que está pasando aquí. Parece que
Eso se ve muy circular.
La respuesta es que las dos ecuaciones anteriores no son las definiciones de
sólo están ecuaciones que relacionan los dos. Usted es libre de elegir su propio paquete de ondas a dar forma a sí mismo - por ejemplo, puede especificar la forma
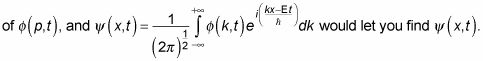
He aquí un ejemplo en el que se obtiene el hormigón, la selección de una forma real paquete de ondas. Elija un paquete llamado ola de Gauss, que se puede ver en la figura - localizado en un solo lugar, cerca de cero en los demás.
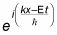
La amplitud
usted puede elegir para este paquete de ondas es
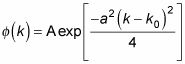
Se empieza por la normalización
para determinar que A es. He aquí cómo funciona:
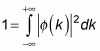
Sustituyendo en
le da esta ecuación:
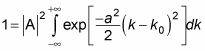
Hacer la integral (que significa mirar hacia arriba en las tablas matemáticas) le da la
siguiendo:
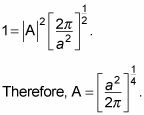
Así que aquí está la función de onda:
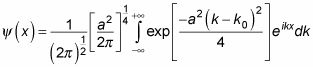
Esta pequeña joya de una integral se puede evaluar para darle el siguiente:
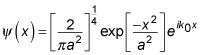
Así que esa es la función de onda para este paquete de ondas gaussiano (Nota: La exp [-X2/la2] Es la parte de Gauss que da el paquete de ondas la forma distintiva que se ve en la figura) - y es ya normalizada.
Ahora usted puede utilizar esta función paquete de ondas para determinar la probabilidad de que la partícula estará en, por ejemplo, la región
La probabilidad es
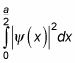
En este caso, la integral es
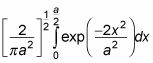
Y esto resulta ser
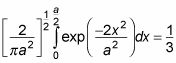
Por lo tanto la probabilidad de que la partícula estará en la región
¡Guay!
-
Aplicando la ecuación radial fuera de la plaza, así -
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo -
Cómo física cuántica convierte el impulso y la posición en probabilidades -
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones -
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes -
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
Cómo relacionar la amplitud de dispersión y la sección transversal diferencial de partículas spinless La amplitud de dispersión de partículas spinless es crucial para la comprensión de dispersión desde el punto de vista de la física cuántica. Para ver esto, eche un vistazo a las densidades de corriente, Jinc (la densidad de flujo de una…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
Fórmulas onda Luz y Óptica Las ondas de luz - es decir, las ondas electromagnéticas - comportarse como otras ondas: Pueden reflejar, refractar (curva), e interferir entre sí. Estas son algunas de las fórmulas de onda que son útiles cuando se trabaja con la óptica. Usted…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…
Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que…
La teoría de cuerdas y las olas Waves (como solemos pensar en ellos) se mueven a través de algún tipo de medio. Si se deslice por el final de un salto de la cuerda o cadena, una ola se mueve a lo largo de la cuerda o cadena. Ondas se mueven a través del agua, o las ondas de…
La teoría de cuerdas: el experimento de la doble rendija Sin la física cuántica, no podría existir la teoría de cuerdas. He aquí un vistazo a cómo la teoría cuántica permite objetos para actuar como partículas y ondas. El experimento que demostró que la luz actúa como una ola fue la experimento…
La teoría de cuerdas: la función de onda cuántica La solución al problema del experimento rendija doble, un concepto en el corazón de los orígenes de la teoría de cuerdas y una consecuencia directa de este primer trabajo en la física cuántica, tomó la forma de la función de onda cuántica,…