Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger
Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m
en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que resuelve para grandes y pequeños r:
Debido a que el Schr # 246-dinger ecuación contiene términos que implican cualquiera R o r pero no ambos, la forma de esta ecuación indica que es una ecuación diferencial separable. Y eso significa que usted puede buscar una solución de la siguiente forma:
Sustituyendo la ecuación anterior en la que antes de que te da el siguiente:
Y dividiendo esta ecuación por
te dio
Esta ecuación tiene términos que dependen de cualquiera
pero no ambos. Esto significa que puede separar esta ecuación en de dos ecuaciones, como este (donde la energía total, E, es igual a ER + Er):
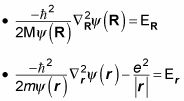
Multiplicando
te dio
Y multiplicando
te dio
Ahora se puede resolver r, pequeños y grandes.
Despejando pequeña r
El Schr # 246-dinger ecuación para
es la función de onda para una partícula inventada de la masa m (en la práctica,
es bastante cerca de
por lo que la energía, Er, es bastante cercano a la energía del electrón). Aquí está la Schr # 246-dinger ecuación para
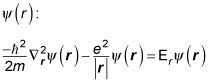
Puede romper la solución,
en una parte radial y una parte angular:
La parte angular de
se compone de armónicos esféricos,
así que está bien esa parte. Ahora usted tiene que resolver para la parte radial, Rnl(r). Esto es lo que la ecuación # 246-dinger Schr se convierte para la parte radial:
dónde
Para resolver esta ecuación, que eche un vistazo a los dos casos - donde r es muy pequeño y donde r es muy grande. Ponerlos juntos le da la forma aproximada de la solución.
Despejando grande r
Por muy grande r,
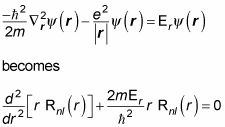
Debido a que el electrón se encuentra en un estado ligado en el átomo de hidrógeno, E lt; 0- por lo tanto, la solución a la ecuación anterior es proporcional a
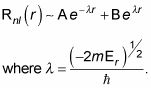
Tenga en cuenta que
diverge como r tiende a infinito debido a la
plazo, por lo B debe ser igual a cero. Eso significa que
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…