Cómo determinar las energías permitidas de un átomo de hidrógeno
Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito es
dónde
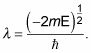
Sustituyendo
en la ecuación de cuantificación condición que dicta la siguiente:
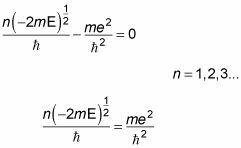
Ahora a resolver por la energía, E. La cuadratura ambos lados de la ecuación anterior le da
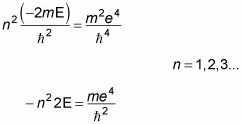
Así que aquí está la energía, E (Nota: Debido a que E depende del número cuántico principal, se cambia el nombre que En):
Los físicos suelen escribir este resultado en términos del radio de Bohr - el radio orbital que Niels Bohr calculó para el electrón en un átomo de hidrógeno, r0. El radio de Bohr es
Y en términos de r0, esto es lo que En es igual a:
El estado de la tierra, donde n = 1, resulta ser sobre E = -13,6 eV.
Tenga en cuenta que esta energía es negativa porque el electrón está en un estado ligado - habría que añadir energía al electrón para liberarlo del átomo de hidrógeno. Éstos son el primer y segundo estados excitados:
En primer estado excitado, n = 2: E = -3.4 eV
En segundo estado excitado, n = 3: E = -1.5 eV
Así que ahora ha utilizado la condición de cuantización, que es
para determinar los niveles de energía del átomo de hidrógeno.
-
Estructura atómica: el modelo de Bohr -
Los enlaces covalentes: un ejemplo de hidrógeno -
Isótopos: diferentes tipos de átomos -
Elementos científicos y electrónica -
Calcular la distancia de un electrón desde el protón de un átomo de hidrógeno -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, es necesario juntar las soluciones para los pequeños r y grandes r. La ecuación Schr # 246-dinger le da una solución a la radial Schr # 246-dinger…
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno Usando la ecuación # 246-dinger Schröder dice que casi todo lo que necesitas saber sobre el átomo de hidrógeno, y todo se basa en una sola hipótesis: que la función de onda debe ir a cero r va hasta el infinito, que es lo que hace que la…
¿Cómo un aumento en r afecta la apariencia de las funciones de onda de hidrógeno En un átomo de hidrógeno, las funciones de onda cambian a medida que cambia el radio orbital, r. Entonces, ¿qué se ven las funciones de onda del hidrógeno como? Dado queSe ve como esto:Aquí están algunas otras funciones de onda de…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo calcular la degeneración de energía de un átomo de hidrógeno en términos de n, l, m y Cada estado cuántico del átomo de hidrógeno se especifica con tres números cuánticos: n (el número cuántico principal), l (el número cuántico del momento angular del electrón), y m (el z componente del momento angular del…
Cómo calcular el espín de un electrón en un átomo de hidrógeno Al calcular el espín de un electrón en un átomo de hidrógeno, es necesario para permitir el giro del electrón, que proporciona estados cuánticos adicionales. Dada la siguiente ecuación, donde la función de onda del átomo de hidrógeno es un…
¿Cómo encontrar los niveles de energía cuadrados así En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.La ecuacionle dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y…
¿Cómo mantener una función de r finito cuando r tiende a infinito En la física cuántica, la hora de encontrar la solución para una ecuación radial para un átomo de hidrógeno, que necesita para mantener la función de r finito como r tiende a infinito para evitar que la solución se vuelva no físico. Usted…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…