¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro
Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la siguiente figura. Aquí, R es la coordenada del núcleo (con respecto al centro de masa), r1 es la coordenada de la primera de electrones (en relación con el centro de masa), r2 la coordenada del segundo electrón, y así sucesivamente.
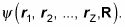
Si usted tiene Z electrones, la función de onda que parece
Y la energía cinética de los electrones y el núcleo se ve así:
Y la energía potencial del sistema se ve así:
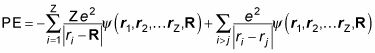
Así que la adición de las dos ecuaciones anteriores, esto es lo que te pasa por la energía total (E = KE + PE) de un átomo de multi-partículas:
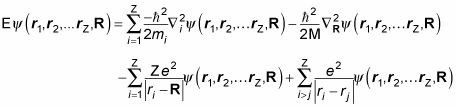
Bien, ahora que parece un lío adecuada. ¿Quieres ganar el premio Nobel de física? Sólo llegar a la solución general de la ecuación anterior. Como es siempre el caso cuando se tiene un sistema de múltiples partículas en el que las partículas interactúan entre sí, no se puede dividir esta ecuación en un sistema de N ecuaciones independientes.
En los casos en que las N partículas de un sistema de múltiples partículas no interactúan entre sí, donde se puede desconectar el Schr # 246-dinger ecuación en un conjunto de N ecuaciones independientes, las soluciones pueden ser posibles. Pero cuando las partículas interactúan y la Schr # 246-dinger ecuación depende de esas interacciones, no se puede resolver esa ecuación por cualquier número significativo de partículas.
Sin embargo, eso no significa que todo esté perdido por cualquier medio. Todavía se puede decir mucho acerca de ecuaciones como éste si eres inteligente - y todo comienza con un examen de la simetría de la situación.
-
Conceptos Química: niveles de energía y orbitales - Fundamentos Electrónica: carga eléctrica
- Elementos científicos y electrónica
-
Los fermiones y bosones -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno -
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo distinguir partículas en un sistema multi-partícula Mecánica cuántica, las partículas idénticas en un sistema de múltiples partículas no lo conservan su individualidad en términos de cualquier, cantidad observable medible. Se pierde la individualidad de partículas idénticas tan pronto como…
¿Cómo encontrar los niveles de energía cuadrados así En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.La ecuacionle dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y…
¿Cómo encontrar la energía total de un sistema de múltiples partículas El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…
Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que…
La teoría de cuerdas y el modelo atómico He aquí una breve exploración del Modelo Estándar de la física de partículas y cómo se relaciona con la teoría de cuerdas. Cualquier teoría de la secuencia completa tendrá que incluir las características del Modelo Estándar y también se…