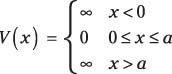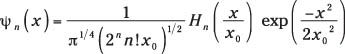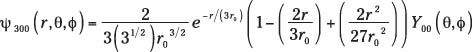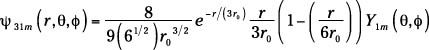El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la partícula - donde está, lo que su impulso es, y así sucesivamente.
En la siguiente versión de la Schr # 246-dinger ecuación, el primer término representa la energía cinética y el segundo término representa la energía potencial:
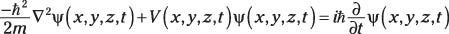
dónde
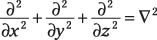
Atrapando las partículas en la Plaza Bueno Potenciales: funciones de onda
Uno de los problemas más fundamentales de la física cuántica con ofertas de partículas atrapadas en un nivel submicroscópico en una plaza bien. El pozo cuadrado es siempre un problema favorito en las clases de mecánica cuántica porque la función de onda funciona tan bien.
El pozo cuadrado tiene muchas variaciones - usted puede tener pozos cuadrados que son simétricas alrededor del origen, que tienen paredes infinitas, que tienen paredes finitas, y más. Aquí está la plaza bien en su forma más básica:
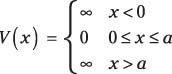
Se trata de una sola dimensión, así, por lo que está en cuestión sólo con el X dirección-, por lo tanto, la Schr # 246-dinger ecuación es la siguiente:
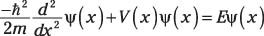
La función de onda se ve así:
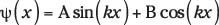
donde A y B son constantes.
Funciones de onda para Quantum armónicas Osciladores
Osciladores armónicos submicroscópicas son problemas de la física cuántica populares porque osciladores armónicos son sistemas relativamente simples - la fuerza que mantiene una partícula unida aquí es proporcional a la distancia a la que la partícula es desde el punto de equilibrio.
Aquí está el oscilador armónico en su forma más simple:
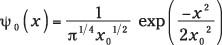
dónde
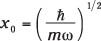
Y aquí está la inmediatamente superior estado:
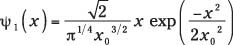
En general, se puede utilizar la siguiente ecuación para las funciones de onda, donde Hn es un polinomio de Hermite:
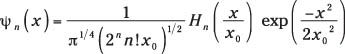
dónde
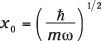
La parte angular de la función de onda: Listado de armónicos esféricos
Funciones de onda del hidrógeno: Single-Electrón Los átomos en la Física Cuántica