La determinación de la parte radial de una función de onda
En la física cuántica, se puede determinar la parte radial de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte radial (que depende de la forma del potencial) y una parte angular, que es un armónico esférico.
Usted puede dar a la parte radial de la función de onda del nombre Rnl(r), dónde n es un número cuántico correspondiente al estado cuántico de la parte radial de la función de onda y l es el número cuántico total del momento angular. La parte radial es simétrica con respecto a los ángulos, por lo que no puede depender de m, el número cuántico del z componente del momento angular. En otras palabras, la función de onda para las partículas en los potenciales centrales se parece a la siguiente ecuación en coordenadas esféricas:
El siguiente paso es resolver para Rnl(r) en general. Sustituyendo
partir de la ecuación anterior en el Schr # 246-dinger ecuación,
te dio
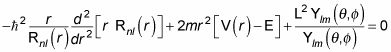
Bueno, ¿qué se puede hacer esto? En primer lugar, tenga en cuenta que los armónicos esféricos son funciones propias de L2 (esa es la razón de su uso), con valor propio
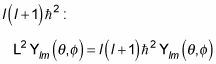
Así que el último término de esta ecuación es simplemente
Eso significa que
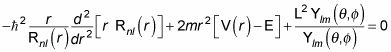
toma la forma
que es igual
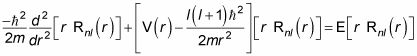
La ecuación anterior es el que se utiliza para determinar la parte radial de la función de onda, Rnl(r). Se llama la ecuación radial para un potencial central.
Al resolver la ecuación radial para Rnl(r), A continuación, puede encontrar
porque ya sabes
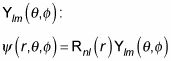
Por lo tanto, usted es simplemente la búsqueda de la solución a la ecuación radial.
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
La aplicación de las funciones de Bessel y Neumann esféricas para una partícula libre -
Aplicando la ecuación radial en el interior del pozo cuadrado -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación
La determinación de la parte angular de una función de onda En la física cuántica, se puede determinar la parte angular de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte…
Encontrar los límites de rho pequeños y grandes de una partícula libre En la física cuántica, se pueden encontrar los límites de rho pequeños y grandes de una partícula libre. De acuerdo con la ecuación de Bessel esférica, la parte radial de la función de onda para una partícula libre se ve así:Echa un…
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno Usando la ecuación # 246-dinger Schröder dice que casi todo lo que necesitas saber sobre el átomo de hidrógeno, y todo se basa en una sola hipótesis: que la función de onda debe ir a cero r va hasta el infinito, que es lo que hace que la…
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
¿Cómo un aumento en r afecta la apariencia de las funciones de onda de hidrógeno En un átomo de hidrógeno, las funciones de onda cambian a medida que cambia el radio orbital, r. Entonces, ¿qué se ven las funciones de onda del hidrógeno como? Dado queSe ve como esto:Aquí están algunas otras funciones de onda de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
¿Cómo mantener una función de r finito cuando r tiende a infinito En la física cuántica, la hora de encontrar la solución para una ecuación radial para un átomo de hidrógeno, que necesita para mantener la función de r finito como r tiende a infinito para evitar que la solución se vuelva no físico. Usted…
Cómo normalizar la función de onda en un potencial cuadro En el curso de física cuántica, se le puede pedir a normalizar la función de onda en un potencial cuadro. He aquí un ejemplo: considere la función de ondaen el X dimensión, tiene esto para la ecuación de onda:Así que la función de onda es…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…