¿Cómo mantener una función de r finito cuando r tiende a infinito
En la física cuántica, la hora de encontrar la solución para una ecuación radial para un átomo de hidrógeno, que necesita para mantener la función de r finito como r tiende a infinito para evitar que la solución se vuelva no físico. Usted puede lograr esto poniendo restricciones sobre los valores permitidos de la energía, y haciendo que la solución para la ecuación radial para ir a cero r va hasta el infinito.
El problema de tener
ir hasta el infinito como r va a mentiras infinito en la forma que usted asume para f (r), cual es
La solución es decir que esta serie de potencias debe terminar en un determinado índice, que se llama a N. N se llama número cuántico radial. Así que esta ecuación se convierte en la siguiente (nota que la suma es ahora a N, no infinito):
Para esta serie para terminar, laN + 1, laN + 2, laN + 3, y así sucesivamente deben ser todos cero. La relación de recurrencia para los coeficientes lak es
por laN + 1 que es cero, el factor multiplicador lak-1 debe ser cero para k = N + 1, lo que significa que
Sustituyendo en k = N + 1 le da
Y dividiendo por 2 le da
Haciendo la sustitución
dónde n se llama la número cuántico principal, te dio
Esta es la condición de cuantización que deben cumplirse si la serie para f (r) Es ser finito, lo que debe ser, física:
Porque
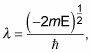
la ecuacion
pone restricciones en los valores permitidos de la energía.
-
Cómo r calcula valores infinitos, no definidos, y que faltan -
En la econometría, la función inversa limita el valor de la variable dependiente -
Evaluación de límites en el cálculo -
Expresar y se aproximan a las funciones utilizando la serie de Taylor -
¿Cómo resolver un problema de límite de plug-and-chu -
Cómo utilizar la prueba de comparación límite para determinar si una serie converge
Múltiplos gráfica de la función tangente En trigonometría, valores tangentes van desde menos infinito hasta el infinito positivo. Así que cuando usted multiplica toda la función tangente de un número, esto es lo que sucede: Si se multiplica por un número mayor que 1, la función se…
Distribuciones de probabilidad continuas Cuando se trabaja con distribuciones de probabilidad continuas, las funciones pueden tomar muchas formas. Estos incluyen uniforme continua, exponencial, normal, normal estándar (Z), la aproximación binomial, Poisson aproximación, y distribuciones…
Aplicando la ecuación radial fuera de la plaza, así En la física cuántica, se puede aplicar la ecuación radial fuera de un pozo cuadrado (donde el radio es mayor que la). En la región r > la, la partícula es igual que una partícula libre, así que esto es lo que la ecuación radial se ve así:A…
Aplicando la ecuación radial en el interior del pozo cuadrado En la física cuántica, se puede aplicar la ecuación radial dentro de un pozo cuadrado (donde el radio es mayor que cero y menor que la). Para un cuadrado esférica pozo de potencial, esto es lo que la ecuación radial parece para la región 0 lt;…
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, es necesario juntar las soluciones para los pequeños r y grandes r. La ecuación Schr # 246-dinger le da una solución a la radial Schr # 246-dinger…
La determinación de la parte radial de una función de onda En la física cuántica, se puede determinar la parte radial de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte…
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo finito es la teoría de cuerdas? Una de las críticas que ha surgido en gran medida desde Smolin de El problema con la Física es la idea de que la teoría de cuerdas no es necesariamente una teoría finita. Recuerde que esta es una de las características clave en apoyo de la…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar los niveles de energía cuadrados así En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.La ecuacionle dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…