¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito
En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:
La función de onda es una onda sinusoidal, yendo a cero en X = 0 y X = la. Usted puede ver las dos primeras funciones de onda trazados en la siguiente figura.
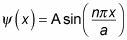
La normalización de la función de onda le permite resolver el A. constante desconocida En una función normalizada, la probabilidad de encontrar la partícula entre
se suma a 1 al integrar en toda la plaza, así, X = 0 a X = la:
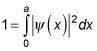
Sustituyendo
le da la siguiente:
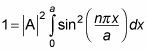
Esto es lo que la integral de esta ecuación es igual a:
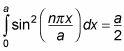
Así que a partir de la ecuación anterior,
Resuelva para A:
Por lo tanto, aquí está la ecuación de onda normalizada con el valor de A enchufado:
Y esa es la función de onda normalizada para una partícula en un cuadrado infinito también.
-
Aplicando la ecuación radial fuera de la plaza, así -
Aplicando la ecuación radial en el interior del pozo cuadrado -
Crear funciones de onda simétricas y antisimétricos por unos sistemas de tres o más de partículas -
Crear funciones de onda simétricas y antisimétricas para un sistema de dos partículas -
Crear funciones de onda simétricas y antisimétricos para cualquier sistema de partículas n -
La determinación de la parte radial de una función de onda
Encontrar los límites de rho pequeños y grandes de una partícula libre En la física cuántica, se pueden encontrar los límites de rho pequeños y grandes de una partícula libre. De acuerdo con la ecuación de Bessel esférica, la parte radial de la función de onda para una partícula libre se ve así:Echa un…
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
Cómo normalizar la función de onda en un potencial cuadro En el curso de física cuántica, se le puede pedir a normalizar la función de onda en un potencial cuadro. He aquí un ejemplo: considere la función de ondaen el X dimensión, tiene esto para la ecuación de onda:Así que la función de onda es…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…