Crear funciones de onda simétricas y antisimétricas para un sistema de dos partículas
Si su instructor de la física cuántica le pide que cree funciones de onda simétricas y antisimétricos para un sistema de dos partículas, se puede comenzar con las funciones de onda-partícula:
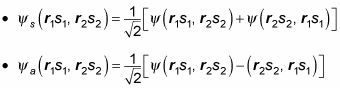
Por analogía, aquí está la función de onda simétrica, compuesta de dos funciones de onda-partícula individual:
Y aquí está la función de onda antisimétrica, formado por las dos funciones de onda-partícula individual:
dónde nyo representa todos los números cuánticos del yoº partícula.
Nota en particular, que
cuando n1 = n2- en otras palabras, la función de onda antisimétrica desvanece cuando las dos partículas tienen el mismo conjunto de números cuánticos - es decir, cuando están en el mismo estado cuántico. Esa idea tiene importantes ramificaciones físicas.
También puede escribir
como éste, donde P es el operador de permutación, que toma la permutación de su argumento:
Y también en cuenta que puede escribir
Me gusta esto:
donde el término (-1)P es 1, incluso para permutaciones (donde se intercambia tanto r1s1 y r2s2 y tambien n1 y n2) Y -1 para permutaciones impares (donde intercambias r1s1 y r2s2 pero no n1 y n2- o intercambias n1 y n2 pero no r1s1 y r2s2).
De hecho, la gente a veces escriben
en forma determinante como esto:
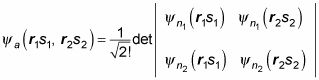
Tenga en cuenta que este determinante es cero si n1 = n2.
-
Aplicando la ecuación radial fuera de la plaza, así -
Crear funciones de onda simétricas y antisimétricos por unos sistemas de tres o más de partículas -
Crear funciones de onda simétricas y antisimétricos para cualquier sistema de partículas n -
La determinación de la parte angular de una función de onda -
La determinación de los niveles de energía de una partícula en un potencial cuadro -
La determinación de la parte radial de una función de onda
Encontrar los límites de rho pequeños y grandes de una partícula libre En la física cuántica, se pueden encontrar los límites de rho pequeños y grandes de una partícula libre. De acuerdo con la ecuación de Bessel esférica, la parte radial de la función de onda para una partícula libre se ve así:Echa un…
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer a encontrar la ecuación de energía total para los problemas de partículas libres tridimensionales. La energía total de la partícula libre es la suma de la energía en tres…
¿Cómo un aumento en r afecta la apariencia de las funciones de onda de hidrógeno En un átomo de hidrógeno, las funciones de onda cambian a medida que cambia el radio orbital, r. Entonces, ¿qué se ven las funciones de onda del hidrógeno como? Dado queSe ve como esto:Aquí están algunas otras funciones de onda de…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
¿Cómo clasificar simétrica y funciones de onda antisimétrica Usted puede determinar lo que ocurre con la función de onda cuando cambias partículas en un átomo de múltiples partículas. Si la función de onda es simétrica o antisimétrica en esas operaciones que da una idea de si dos partículas pueden…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
¿Cómo encontrar la energía total de un sistema de múltiples partículas El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…