¿Cómo clasificar simétrica y funciones de onda antisimétrica
Usted puede determinar lo que ocurre con la función de onda cuando cambias partículas en un átomo de múltiples partículas. Si la función de onda es simétrica o antisimétrica en esas operaciones que da una idea de si dos partículas pueden ocupar el mismo estado cuántico.
Dado que Pij2 = 1, tenga en cuenta que si una función de onda es una función propia de Pij, a continuación, los posibles valores propios son 1 y -1. Es decir, para
una función propia de Pij Parece que
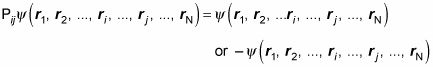
Eso significa que hay dos tipos de funciones propias del operador cambiario:
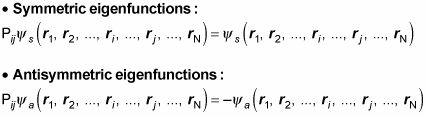
Ahora echa un vistazo a algunos simétrica y algunas funciones propias antisimétricos. ¿Qué tal este - es simétrica o antisimétrica?
Puede aplicar el operador cambiario P12:
Tenga en cuenta que debido a
es una onda simétrica funcionalidad que se debe
¿Qué tal esta función de onda?
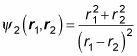
Una vez más, aplicar el operador de cambio, P12:
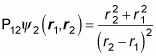
Está bien, pero debido
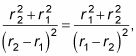
tu sabes
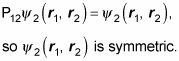
Aquí hay otro:
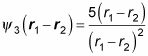
Ahora aplique P12:
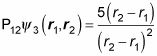
¿Cómo esa ecuación se compara con el original? Bien,
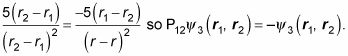
Por Consiguiente,
es antisimétrica.
¿Qué tal este?
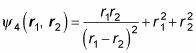
Para averiguarlo, aplicar P12:
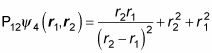
Muy bien - ¿cómo se compara esto con la ecuación original?
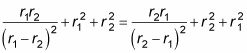
Bueno ;
es simétrica.
Usted puede pensar que tiene este proceso hasta bastante bien, pero ¿qué pasa con esta nueva función de onda?
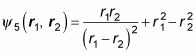
Comience por la aplicación de P12:
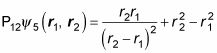
Entonces, ¿cómo se comparan estas dos ecuaciones?
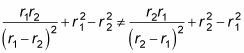
Eso es,
no es ni simétrica ni antisimétrica. En otras palabras,
no es una función propia del P12 operador cambiario.
-
Aplicando la ecuación radial fuera de la plaza, así -
Crear funciones de onda simétricas y antisimétricos por unos sistemas de tres o más de partículas -
Crear funciones de onda simétricas y antisimétricas para un sistema de dos partículas -
Crear funciones de onda simétricas y antisimétricos para cualquier sistema de partículas n -
La determinación de la parte angular de una función de onda -
La determinación de la parte radial de una función de onda
Encontrar los límites de rho pequeños y grandes de una partícula libre En la física cuántica, se pueden encontrar los límites de rho pequeños y grandes de una partícula libre. De acuerdo con la ecuación de Bessel esférica, la parte radial de la función de onda para una partícula libre se ve así:Echa un…
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
¿Cómo un aumento en r afecta la apariencia de las funciones de onda de hidrógeno En un átomo de hidrógeno, las funciones de onda cambian a medida que cambia el radio orbital, r. Entonces, ¿qué se ven las funciones de onda del hidrógeno como? Dado queSe ve como esto:Aquí están algunas otras funciones de onda de…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
¿Cómo encontrar las correcciones de primer orden a los niveles de energía y funciones de onda En la física cuántica, con el fin de encontrar las correcciones de primer orden a los niveles de energía y funciones de onda de un sistema perturbado, En, es necesario calcular E(1)n, al igual queAsique como haces eso? Usted comienza con tres…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
Cómo normalizar la función de onda en un potencial cuadro En el curso de física cuántica, se le puede pedir a normalizar la función de onda en un potencial cuadro. He aquí un ejemplo: considere la función de ondaen el X dimensión, tiene esto para la ecuación de onda:Así que la función de onda es…
Cómo cambiar la simétrica cuadrada bien en torno al origen Pozos cuadrados Infinitas, en el que las paredes van a infinito, son uno de los favoritos en los problemas de la física cuántica. En algunos casos, es posible que desee cambiar las cosas para que el pozo cuadrado es simétrica alrededor del…