La determinación de los niveles de energía de una partícula en un potencial cuadro
En la física cuántica, para poder determinar los niveles de energía de una partícula en un potencial cuadro, usted necesita un valor exacto para X (X) - No sólo uno de los términos de las constantes A y B. Usted tiene que utilizar las condiciones de contorno para encontrar A y B. ¿Cuáles son las condiciones de frontera? La función de onda debe desaparecer en los límites de la caja, por lo que
X (0) = 0
X (LX) = 0
Por lo tanto el hecho de que
le dice de inmediato que B debe ser 0, ya que cos (0) = 1. Y el hecho de que X (LX) = 0 le dice que X (LX) = A sen (kXLX) = 0. Debido a que el seno es 0 cuando su argumento es un múltiplo de
esto significa eso
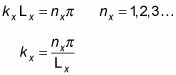
Y por eso
esto significa que
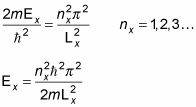
Esa es la energía en el X componente de la función de onda, correspondiente a los números cuánticos 1, 2, 3, y así sucesivamente. La energía total de una partícula de masa m dentro de la caja de potencial es E = EX + Ey + Ez. Siguiendo
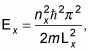
usted tiene esto para Ey y Ez:
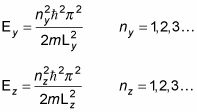
Por lo tanto la energía total de la partícula es E = EX + Ey + Ez, que es igual a esto:
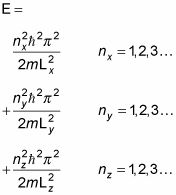
Y ahí lo tienen la energía total de una partícula en el potencial de la caja.
-
Aplicando la ecuación radial fuera de la plaza, así -
Crear funciones de onda simétricas y antisimétricas para un sistema de dos partículas -
Encontrar los límites de rho pequeños y grandes de una partícula libre -
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones -
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo -
Cómo partículas túnel a través de barreras potenciales que tienen una mayor energía
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
¿Cómo encontrar los niveles de energía cuadrados así En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.La ecuacionle dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
¿Cómo encontrar la energía total de un sistema de múltiples partículas El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número…
Cómo interpretar diagramas de energía en la física En física, la energía potencial de un objeto depende de su posición. Una roca tiene más energía potencial cuando está en la cima de una colina que cuando está rodando. En su clase de física, se le puede pedir a interpretar o dibujar un…
Cómo normalizar la función de onda en un potencial cuadro En el curso de física cuántica, se le puede pedir a normalizar la función de onda en un potencial cuadro. He aquí un ejemplo: considere la función de ondaen el X dimensión, tiene esto para la ecuación de onda:Así que la función de onda es…
¿Cómo trabajar con un potencial cúbico En la física cuántica, cuando se trabaja con un potencial de caja, usted puede hacer las cosas más simples suponiendo que el cuadro es en realidad un cubo. En otras palabras, L = LX = Ly = Lz. Cuando el cuadro es un cubo, la ecuación de la…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
La teoría de cuerdas: acceso a universos paralelos con túnel cuántico En la teoría de cuerdas, una proceso de obtención de un universo a otro sería el uso de la propiedad de túnel cuántico, que es donde se permite que una partícula " salto " de un lugar a otro a través de una barrera.El principio de…