¿Cómo encontrar los niveles de energía cuadrados así
En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.
La ecuacion
le dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y B. ¿Cuáles son las condiciones de frontera? La función de onda debe desaparecer en los límites de un cuadrado infinito y, por lo
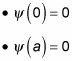
El hecho de que
le informa de inmediato de que B debe ser cero porque cos (0) = 1. Y el hecho de que
le dice que
Debido sine es cero cuando su argumento es un múltiplo de
esto significa eso
Tenga en cuenta que aunque n = 0 es técnicamente una solución, se produce
para todos X, que no es normalizable, por lo que no es una solución física - las soluciones físicas comienzan con n = 1.
Esta ecuación también se puede escribir como
Y por eso
usted tiene la siguiente ecuación, donde n = 1, 2, 3, ... - esos son los estados de energía permitidos. Estos son estados cuantificados, que corresponden a los números cuánticos 1, 2, 3, y así sucesivamente:
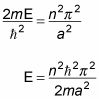
Tenga en cuenta que el primer estado físico corresponde a n = 1, lo que le da la siguiente ecuación:
Este es el estado físico más bajo que las partículas pueden ocupar. Sólo por diversión, poner algunos números en esto, asumiendo que se dispone de un electrón, la masa
confinado a un pozo cuadrado infinito de ancho de la orden del Radio de Bohr (el radio medio de la órbita de un electrón en un átomo de hidrógeno) - digamos
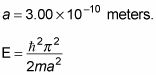
le da esta energía para el estado fundamental:
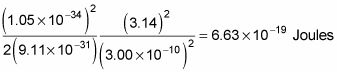
Esa es una cantidad muy pequeña, alrededor de 4 electronvoltios (eV - la cantidad de energía que se gana electrones caen a través de 1 voltio). Aun así, ya está en el orden de la energía del estado fundamental de un electrón en el estado fundamental del átomo de hidrógeno (13,6 eV), por lo que se puede decir que está sin duda en la derecha estadio física cuántica ahora.
-
Estructura atómica: el modelo de Bohr -
Aplicando la ecuación radial fuera de la plaza, así -
Calcular la distancia de un electrón desde el protón de un átomo de hidrógeno -
La determinación de los niveles de energía de una partícula en un potencial cuadro -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno -
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo calcular la degeneración de energía de un átomo de hidrógeno en términos de n, l, m y Cada estado cuántico del átomo de hidrógeno se especifica con tres números cuánticos: n (el número cuántico principal), l (el número cuántico del momento angular del electrón), y m (el z componente del momento angular del…
Cómo calcular el espín de un electrón en un átomo de hidrógeno Al calcular el espín de un electrón en un átomo de hidrógeno, es necesario para permitir el giro del electrón, que proporciona estados cuánticos adicionales. Dada la siguiente ecuación, donde la función de onda del átomo de hidrógeno es un…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar las correcciones de segundo orden a los niveles de energía y funciones de onda En la física cuántica, con el fin de encontrar las correcciones de segundo orden a los niveles de energía y funciones de onda de un sistema perturbado, En, es necesario calcular E(2)n, al igual queAsique como haces eso? Usted comienza con tres…
¿Cómo mantener una función de r finito cuando r tiende a infinito En la física cuántica, la hora de encontrar la solución para una ecuación radial para un átomo de hidrógeno, que necesita para mantener la función de r finito como r tiende a infinito para evitar que la solución se vuelva no físico. Usted…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica y el hamiltoniano Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…