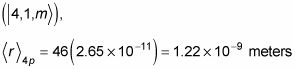Calcular la distancia de un electrón desde el protón de un átomo de hidrógeno
Cuando usted quiere encontrar en un electrón es en un momento dado en un átomo de hidrógeno, lo que en realidad estás haciendo es encontrar en qué medida el electrón es del protón. Usted puede encontrar el valor esperado de r, eso es,
la siguiente expresión representa la probabilidad de que el electrón se encuentre en el elemento espacial d3r:
En coordenadas esféricas,
Así que usted puede escribir
como
La probabilidad de que el electrón está en una cáscara esférica de radio r a r + dr es, por lo tanto
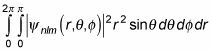
Y por eso
esta ecuación se convierte en la siguiente:
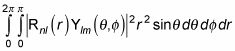
La ecuación anterior es igual a
(Recuerde que el símbolo del asterisco significa el complejo conjugado. Un conjugado complejo voltea el signo que conecta las partes real e imaginaria de un número complejo.)
Armónicos esféricos son normalizados, así que esto solo se hace
Bueno, esa es la probabilidad de que el electrón es el interior de la cáscara esférica de r a r + dr. Así que el valor esperado de r, cual es
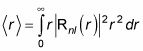
cual es
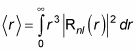
Aquí es donde las cosas se ponen más complejo, ya que Rnl(r) Implica los polinomios de Laguerre. Pero después de un montón de matemáticas, esto es lo que se obtiene:
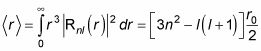
dónde r0 es el radio de Bohr:
El radio de Bohr se trata de
por lo que el valor esperado de la distancia a la electrónica del protón es
Así, por ejemplo, en el 1s estado
el valor esperado de r es igual a
Y en el 4p estado
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica te pide encontrar la función de onda de un átomo de hidrógeno, se puede comenzar con el radial Schr # 246-dinger ecuación, Rnl(r), Que le dice queLa ecuación anterior proviene de resolver el radial Schr…
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno Usando la ecuación # 246-dinger Schröder dice que casi todo lo que necesitas saber sobre el átomo de hidrógeno, y todo se basa en una sola hipótesis: que la función de onda debe ir a cero r va hasta el infinito, que es lo que hace que la…
Encuentra las funciones propias de lz en coordenadas esféricas En algún momento, su instructor física cuántica puede pedirle que encontrar las funciones propias de la Lz en coordenadas esféricas. En coordenadas esféricas, la Lz operador tiene este aspecto:que es la siguiente:Y por esoesta ecuación se…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo calcular la degeneración de energía de un átomo de hidrógeno en términos de n, l, m y Cada estado cuántico del átomo de hidrógeno se especifica con tres números cuánticos: n (el número cuántico principal), l (el número cuántico del momento angular del electrón), y m (el z componente del momento angular del…
Cómo calcular el espín de un electrón en un átomo de hidrógeno Al calcular el espín de un electrón en un átomo de hidrógeno, es necesario para permitir el giro del electrón, que proporciona estados cuánticos adicionales. Dada la siguiente ecuación, donde la función de onda del átomo de hidrógeno es un…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar los niveles de energía cuadrados así En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.La ecuacionle dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y…
¿Cómo encontrar las funciones propias de l2 en coordenadas esféricas Su instructor física cuántica puede pedirle que encontrar las funciones propias de la L2 en coordenadas esféricas. Para ello, se comienza con la función propia deldado que en coordenadas esféricas, la L2 operador tiene este aspecto:Eso es todo…
¿Cómo encontrar el operador adjunto En la física cuántica, a menudo trabaja con adjoints hermitianas. los Operador adjunto - también llamado adjunto o Conjugado hermítica - de un operador A se denotaPara encontrar el operador adjunto, sigue estos pasos:Reemplazar constantes…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…