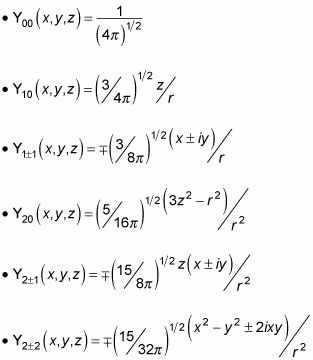¿Cómo encontrar las funciones propias de l2 en coordenadas esféricas
Su instructor física cuántica puede pedirle que encontrar las funciones propias de la L2 en coordenadas esféricas. Para ello, se comienza con la función propia del
dado que en coordenadas esféricas, la L2 operador tiene este aspecto:
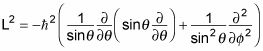
Eso es todo un operador. Y, dado que
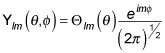
se puede aplicar la L2 operador
que se da la siguiente:
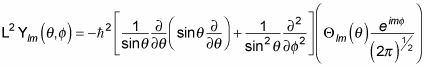
Y por eso
esta ecuación se convierte en
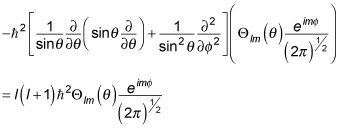
Wow, ¿qué has metido? Cancelación términos y restando la derecha; lado de la izquierda, finalmente, le da esta ecuación diferencial:
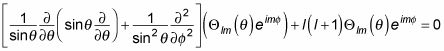
Combinando términos y dividiendo por
le da la siguiente:
Vaca santa! ¿No hay alguien que trató de resolver este tipo de ecuación diferencial antes? Sí hay. Esta ecuación es una ecuación diferencial de Legendre, y las soluciones son bien conocidos. (! ¡Menos mal) En general, las soluciones tienen esta forma:
dónde
es el Función de Legendre.
¿Cuáles son las funciones de Legendre? Puedes empezar por separar la m la dependencia, que funciona de esta manera con las funciones de Legendre:
donde Pl(X) Se llama Legendre polinomio y viene dada por la fórmula de Rodrigues:
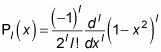
Usted puede utilizar esta ecuación para derivar los primeros polinomios de Legendre como éste:
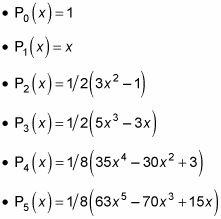
etcétera. Eso es lo que la primera pocos Pl (X) Polinomios parecen. Entonces, ¿qué hacen las funciones de Legendre asociadas, Plm (X) ¿parece? También puede calcularlos. Usted puede comenzar con Pl0 (X), dónde m = 0. Esos son fáciles porque Pl0 (X) = Pl (X), Por lo
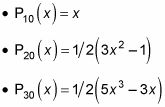
Además, usted puede encontrar que
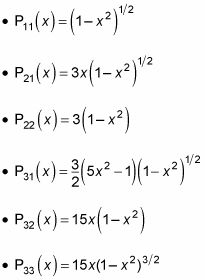
Estas ecuaciones que dan una visión de lo que el Plm funciones parecen, lo que significa que está casi terminado. Como se recordará,
está relacionada con el Plm funciones como éste:
Y ahora usted sabe lo que el Plm funciones parecen, pero lo que hacen Clm, las constantes, se parecen? Tan pronto como usted tiene esos, que tendrá las funciones propias completos del momento angular,
Usted puede ir sobre el cálculo de las constantes de Clm la manera que siempre calcular esas constantes de integración en la física cuántica - a normalizar las funciones propias a 1.
que se parece a esto:
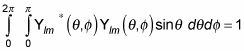
(Recuerde que el símbolo del asterisco significa el complejo conjugado. Un conjugado complejo voltea el signo que conecta las partes real e imaginaria de un número complejo.)
Sustituya los siguientes tres cantidades en esta ecuación:
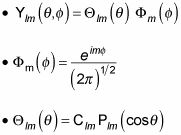
Aparecerá el siguiente:
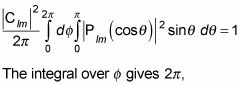
por lo que este se convierte
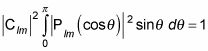
Usted puede evaluar la integral a lo siguiente:
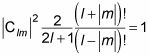
En otras palabras:
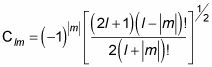
Lo que significa que
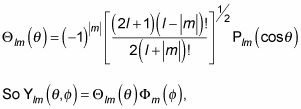
que es la función propia del momento angular en coordenadas esféricas, es
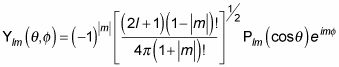
Las funciones dadas por esta ecuación se llaman armónicos esféricos normalizados. Éstos son lo que los primeros armónicos esféricos normalizados parecen:
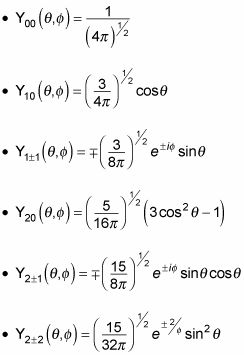
De hecho, puede utilizar estas relaciones para convertir los armónicos esféricos a coordenadas rectangulares:
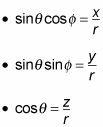
Sustituyendo estas ecuaciones en
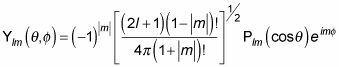
le da los armónicos esféricos en coordenadas rectangulares:
-
¿Cómo encontrar la ecuación de una línea en la TI-84 Plus -
Cómo graficar funciones en la TI-Nspire -
Ecuaciones diferenciales libro para los maniquíes -
Definición de ecuaciones diferenciales homogéneas y no homogéneas -
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden -
Aplicando la ecuación schr & # 246-dinger en tres dimensiones
Aplicando la ecuación radial fuera de la plaza, así En la física cuántica, se puede aplicar la ecuación radial fuera de un pozo cuadrado (donde el radio es mayor que la). En la región r > la, la partícula es igual que una partícula libre, así que esto es lo que la ecuación radial se ve así:A…
La aplicación de las funciones de Bessel y Neumann esféricas para una partícula libre En la física cuántica, puede aplicar las funciones esféricas de Bessel y Neumann para una partícula libre (una partícula que no está limitado por ningún potencial). La función de onda en coordenadas esféricas toma esta forma:yle da los…
Aplicando la ecuación radial en el interior del pozo cuadrado En la física cuántica, se puede aplicar la ecuación radial dentro de un pozo cuadrado (donde el radio es mayor que cero y menor que la). Para un cuadrado esférica pozo de potencial, esto es lo que la ecuación radial parece para la región 0 lt;…
Calcular la distancia de un electrón desde el protón de un átomo de hidrógeno Cuando usted quiere encontrar en un electrón es en un momento dado en un átomo de hidrógeno, lo que en realidad estás haciendo es encontrar en qué medida el electrón es del protón. Usted puede encontrar el valor esperado de r, eso es, , para…
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica te pide encontrar la función de onda de un átomo de hidrógeno, se puede comenzar con el radial Schr # 246-dinger ecuación, Rnl(r), Que le dice queLa ecuación anterior proviene de resolver el radial Schr…
La determinación de la parte angular de una función de onda En la física cuántica, se puede determinar la parte angular de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte…
La determinación de la parte radial de una función de onda En la física cuántica, se puede determinar la parte radial de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte…
Encuentra las funciones propias de lz en coordenadas esféricas En algún momento, su instructor física cuántica puede pedirle que encontrar las funciones propias de la Lz en coordenadas esféricas. En coordenadas esféricas, la Lz operador tiene este aspecto:que es la siguiente:Y por esoesta ecuación se…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
¿Cómo cambiar las coordenadas rectangulares a coordenadas esféricas En la física cuántica, para encontrar las funciones propias reales (no sólo los estados propios) de los operadores de momento angular como L2 y yoz, te apartas de coordenadas rectangulares, X, y, y z, a coordenadas esféricas, ya que va a hacer…
¿Cómo encontrar el operador adjunto En la física cuántica, a menudo trabaja con adjoints hermitianas. los Operador adjunto - también llamado adjunto o Conjugado hermítica - de un operador A se denotaPara encontrar el operador adjunto, sigue estos pasos:Reemplazar constantes…
Cómo relacionar la amplitud de dispersión y la sección transversal diferencial de partículas spinless La amplitud de dispersión de partículas spinless es crucial para la comprensión de dispersión desde el punto de vista de la física cuántica. Para ver esto, eche un vistazo a las densidades de corriente, Jinc (la densidad de flujo de una…