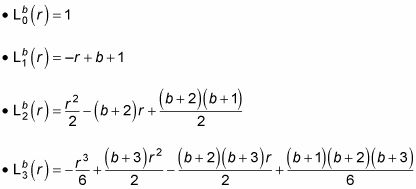Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger
Si su instructor de la física cuántica te pide encontrar la función de onda de un átomo de hidrógeno, se puede comenzar con el radial Schr # 246-dinger ecuación, Rnl(r), Que le dice que
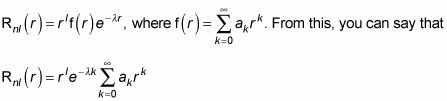
La ecuación anterior proviene de resolver el radial Schr # 246-dinger ecuación:
La solución sólo es bueno para una constante multiplicativa, por lo que añadir una constante, A talesnl (que resulta que dependerá del número cuántico principal n y el número cuántico del momento angular l), Me gusta esto:
A encontrar unnl normalizando Rnl(r).
Ahora tratar de resolver para la Inl(r) Con sólo hacer los cálculos de plano. Por ejemplo, tratar de encontrar R10(r). En este caso, n = 1 y l = 0. Entonces, debido a N + l + 1 = n, usted tiene N = n - l - 1. Así que N = 0 aquí. Eso hace que Rnl(r) se parece a esto:
Y la suma en esta ecuación es igual a
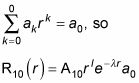
Y por eso l = 0, rl = 1, por lo
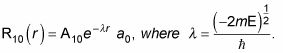
Por lo tanto, usted también puede escribir
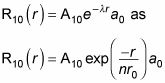
dónde r0 es el radio de Bohr. Para encontrar un10 y la0, a normalizar
a 1, lo que significa la integración
en todo el espacio y el establecimiento el resultado a 1.
y la integración de los armónicos esféricos, tales como Y00, sobre una esfera completa,
le da 1. Por lo tanto, uno se queda con la parte radial de normalizar:
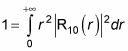
Tapar
dentro
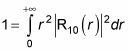
te dio
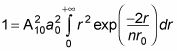
Puede resolver este tipo de una sola pieza con la siguiente relación:
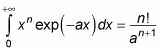
Con esta relación, la ecuación
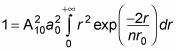
se convierte en
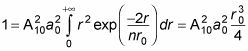
Por Consiguiente,
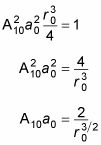
Este es un resultado bastante simple. Porque un10 está ahí para normalizar el resultado, se puede establecer un10 a 1 (esto no sería el caso si
varios términos involucrados). Por Consiguiente,
Eso está bien, y hace R10(r), cual es
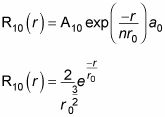
Tu sabes
Y así
se convierte en
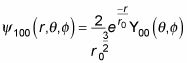
¡Menos mal. En general, esto es lo que la función de onda
parece que para el hidrógeno:
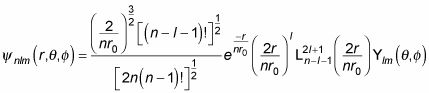
dónde
es un polinomio de Laguerre generalizado. Estos son los primeros polinomios de Laguerre generalizados:
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
Aplicando la ecuación radial en el interior del pozo cuadrado -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…