Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación
Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, es necesario juntar las soluciones para los pequeños r y grandes r. La ecuación Schr # 246-dinger le da una solución a la radial Schr # 246-dinger ecuación para un átomo de hidrógeno de la siguiente manera:
donde f (r) Es una función aún como-indeterminado de r. Su siguiente tarea es determinar f (r), Lo que lo hace mediante la sustitución de esta ecuación en la radial Schr # 246-dinger ecuación, dándole la siguiente:
Realizar la sustitución le da la siguiente ecuación diferencial:
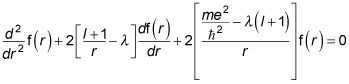
Toda una ecuación diferencial, ¿eh? Pero simplemente sentarse y relajarse - a resolver con una serie de potencias, que es una forma común de resolver ecuaciones diferenciales. Aquí está la forma en serie de potencias de f (r) para usar:
Sustituyendo la ecuación anterior en la anterior le da
Cambiar el índice del segundo mandato de k a k - 1 le da
Debido a que cada término de esta serie tiene que ser cero, usted tiene
Dividiendo por rk-2 te dio
Esta ecuación da la relación de recurrencia de la serie infinita,
Es decir, si usted tiene un coeficiente, puede obtener el siguiente uso de esta ecuación. ¿Qué es lo que usted compra? Bueno, eche un vistazo a la relación de lak/lak-1:
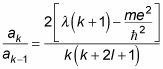
Esto es lo que se aproxima a esta relación como k va hasta el infinito:
Esto se asemeja a la expansión de eX, cual es
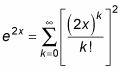
Como para e2X, la relación de términos sucesivos es
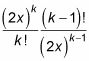
Y en el límite
la relación de coeficientes de expansión sucesivas de e2X enfoques 2 /k:
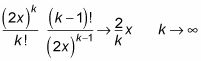
Ese es el caso de e2X. Para f (r), Tienes
Comparando estas dos ecuaciones, es evidente que
La función de onda radial, Rnl(r), Se ve como esto:
dónde
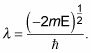
Tapar la forma que tiene para f (r),
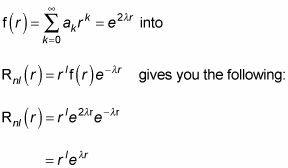
De acuerdo, en caso de que esté muy contento? Bueno no. Esto es lo que la función de onda
Parece que:
Y sustituyendo en su forma de Rnl(r) De esta ecuación que da
-
Definición de ecuaciones diferenciales homogéneas y no homogéneas -
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo mantener una función de r finito cuando r tiende a infinito En la física cuántica, la hora de encontrar la solución para una ecuación radial para un átomo de hidrógeno, que necesita para mantener la función de r finito como r tiende a infinito para evitar que la solución se vuelva no físico. Usted…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…