Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno
En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:
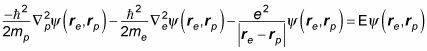
El problema es que usted está tomando en cuenta la distancia que el protón es desde el centro de la masa del átomo, por lo que la matemática es desordenado. Si se va a suponer que el protón es estacionaria y que rp = 0, esta ecuación se vendría abajo a la siguiente, que es mucho más fácil de resolver:
Por desgracia, esa ecuación no es exacta porque ignora el movimiento del protón, por lo que ver la versión más completa de la ecuación en la mecánica cuántica textos.
Para simplificar el Schr # 246-dinger ecuación de costumbre, se cambia al centro de masa coordenadas. El centro de masa del sistema de protón / electrón es en esta ubicación:
Y el vector entre el electrón y el protón es
r = re - rp
El uso de vectores R y r en lugar de re y rp hace que el Schr # 246-dinger ecuación más fácil de resolver. El Laplaciano para R es
Y el Laplaciano de r es
¿Cómo se puede relacionar
a de la ecuación habitual
Después de que el álgebra se asienta, se obtiene
donde M = me + mp es la masa total y
se llama la masa reducida. Cuando juntas las ecuaciones para el centro de la masa, el vector entre el protón y el electrón, la masa total, y m, entonces el Schr # 246-dinger ecuación independiente del tiempo se convierte en la siguiente:
A continuación, dados los vectores, R y r, el potencial está dada por,
El Schr # 246-dinger ecuación se convierte en
Esto se ve más fácil - la principal mejora es que ahora tienes |r| en el denominador del término de energía potencial más que |re - rp|.
Debido a que la ecuación contiene términos que implican cualquiera R o r pero no ambos, la forma de esta ecuación indica que es una ecuación diferencial separable. Y eso significa que usted puede buscar una solución de la siguiente forma:
Sustituyendo la ecuación anterior en la que antes de que te da el siguiente:
Y dividiendo esta ecuación por
te dio
Bien bien bien. Esta ecuación tiene términos que dependen de cualquiera
pero no ambos. Esto significa que puede separar esta ecuación en de dos ecuaciones, como este (donde la energía total, E, es igual a ER + Er):
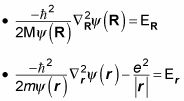
Multiplicando
te dio
Y multiplicando
te dio
Ahora tienes dos Schr # ecuaciones 246-Dinger, que se puede resolver de forma independiente.
-
Equilibrar las ecuaciones químicas -
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Calcula la función de onda de un átomo de hidrógeno utilizando la schr & # ecuación 246-dinger -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo calcular el espín de un electrón en un átomo de hidrógeno Al calcular el espín de un electrón en un átomo de hidrógeno, es necesario para permitir el giro del electrón, que proporciona estados cuánticos adicionales. Dada la siguiente ecuación, donde la función de onda del átomo de hidrógeno es un…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…