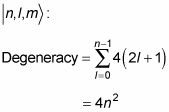Cómo calcular el espín de un electrón en un átomo de hidrógeno
Al calcular el espín de un electrón en un átomo de hidrógeno, es necesario para permitir el giro del electrón, que proporciona estados cuánticos adicionales. Dada la siguiente ecuación, donde la función de onda del átomo de hidrógeno es un producto de partes radiales y angulares,
usted puede añadir una parte de giro, lo que corresponde al spin del electrón, donde s es el spin del electrón y ms es el z componente del giro:
La parte vuelta de la ecuación puede tomar los siguientes valores:
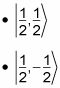
Por lo tanto,
ahora se convierte
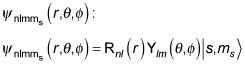
Y esta función de onda puede tomar dos formas diferentes, dependiendo de ms, Me gusta esto:
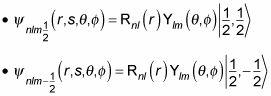
De hecho, puede utilizar la notación de vuelta, donde
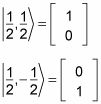
Por ejemplo, para
usted puede escribir la función de onda como
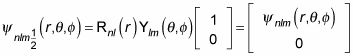
Y para
usted puede escribir la función de onda como
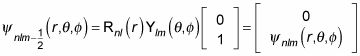
¿Qué hace esto a la degeneración de energía? Si se incluye el espín del electrón, hay dos estados de espín para cada estado
por lo que la degeneración se convierte
Así que si usted incluye espín del electrón, la degeneración de energía del átomo de hidrógeno es 2n2.
De hecho, incluso se puede añadir el espín del protón para la función de onda (aunque la gente no suele hacer eso, porque espín del protón interactúa débilmente con los campos magnéticos aplicados al átomo de hidrógeno). En ese caso, usted tiene una función de onda que se parece a lo siguiente:
dónde se es el spin del electrón, msí es el z componente del espín del electrón, sp es el spin del protón, y msp es el z componente del espín del protón.
Si incluye espín del protón, la función de onda puede ahora tomar cuatro formas diferentes, dependiendo de ms, Me gusta esto:
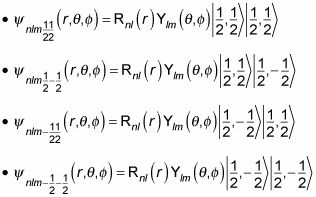
La degeneración ahora debe incluir espín del protón, por lo que es un factor de cuatro para cada
-
Isótopos: diferentes tipos de átomos -
Elementos científicos y electrónica - Hacer imágenes de resonancia magnética para verduras con nanopartículas de óxido de hierro
- 9 constantes de la física para saber
-
Calcular la distancia de un electrón desde el protón de un átomo de hidrógeno -
Los fermiones y bosones
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno Usando la ecuación # 246-dinger Schröder dice que casi todo lo que necesitas saber sobre el átomo de hidrógeno, y todo se basa en una sola hipótesis: que la función de onda debe ir a cero r va hasta el infinito, que es lo que hace que la…
Encuentra el punto que falta con el experimento de Stern-Gerlach El experimento de Stern-Gerlach reveló inesperadamente la existencia de la vuelta atrás en el 1922. Los físicos Otto Stern y Walther Gerlach envió un haz de átomos de plata a través de los polos de un imán - cuyo campo magnético estaba en el…
Cómo el efecto Compton de la luz explica desplazamiento de longitud de onda Aunque Max Planck y Albert Einstein postuló que la luz podía comportarse como tanto una onda y una partícula, fue Arthur Compton quien finalmente demostró que esto era posible. Su experimento involucró esparciendo fotones de electrones, como la…
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo calcular la degeneración de energía de un átomo de hidrógeno en términos de n, l, m y Cada estado cuántico del átomo de hidrógeno se especifica con tres números cuánticos: n (el número cuántico principal), l (el número cuántico del momento angular del electrón), y m (el z componente del momento angular del…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar los niveles de energía cuadrados así En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.La ecuacionle dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
Matrices de Pauli En la física cuántica, cuando se trabaja con estados propios de spin y operadores para partículas de espín 1/2 en términos de matrices, es posible que vea los operadores SX, Sy, y Sz escrito en términos de Pauli matrices,Teniendo en cuenta que…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda pequeña ry r grande utilizando el schr & # ecuación 246-dinger Su instructor física cuántica puede pedirle que resuelva para la función de onda para una partícula inventada de la masa m en un átomo de hidrógeno. Para hacer esto, puede comenzar utilizando un Schr # 246-dinger ecuación modificada que…
Haga girar las matrices y medio En la física cuántica, cuando nos fijamos en los estados propios de spin y operadores para partículas de espín 1/2 en términos de matrices, sólo hay dos estados posibles, girar y girar hacia abajo.Los valores propios de la S2 operador sony los…