Haga girar las matrices y medio
En la física cuántica, cuando nos fijamos en los estados propios de spin y operadores para partículas de espín 1/2 en términos de matrices, sólo hay dos estados posibles, girar y girar hacia abajo.
Los valores propios de la S2 operador son
y los valores propios de la Sz operador son
Puede representar estas dos ecuaciones gráficamente como se muestra en la siguiente figura, donde los dos estados de espín tienen diferentes proyecciones a lo largo del z eje.
En el caso de spin 1/2 matrices, primero Representas a la eigenstate
Me gusta esto:
Y el estado propio
Se ve como esto:
Ahora ¿qué pasa con los operadores de spin como S2? El S2 operador tiene este aspecto en términos de matriz:
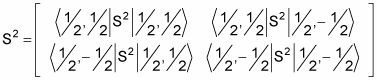
Y esto resulta ser la siguiente:
Del mismo modo, puede representar la Sz operador de esta manera:
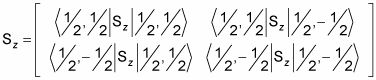
Esto se resuelve a
Utilizando la versión de la matriz de Sz, por ejemplo, se puede encontrar la z componente del giro de, por ejemplo, el estado propio
Encontrar el z componente se ve así:
Poniendo esto en términos de la matriz que le da a este producto matricial:
Esto es lo que se obtiene mediante la realización de la multiplicación de matrices:
Y poniendo esto de nuevo en la notación cado, se obtiene lo siguiente:
¿Qué hay de los operadores de subir y bajar S+ y S-? El S+ operador tiene este aspecto:
Y el operador de la reducción se ve así:
Aquí es en términos de la matriz:
Realizando la multiplicación le da esto:
O en forma cado, es
Guay.
Los fermiones y bosones En analogía con momento angular orbital, se puede asumir que m (el z-eje componente del spin) puede tomar los valores -s, -s + 1, ..., s - 1, y s, dónde s es el número total cuántico de espín. Para los electrones, los físicos Otto Stern y…
Cómo operadores de spin se asemejan a los operadores del momento angular Debido giro es un tipo de momento angular incorporado, operadores de spin tienen mucho en común con los operadores de momento angular orbital. A medida que su instructor de la física cuántica le dirá, hay operadores de spin análogas, S2 y Sz,…
Cómo organizar eingenvectors En la física cuántica, los vectores propios de un operador hermítica definen un conjunto completo de vectores ortonormales - es decir, una base completa para el espacio de estados. Cuando se ve en este " base propia, " que se construye de los…
Cómo calcular el espín de un electrón en un átomo de hidrógeno Al calcular el espín de un electrón en un átomo de hidrógeno, es necesario para permitir el giro del electrón, que proporciona estados cuánticos adicionales. Dada la siguiente ecuación, donde la función de onda del átomo de hidrógeno es un…
Cómo crear estados propios del momento angular Puede crear los estados propios reales, | l, m>, de estados de momento angular en la mecánica cuántica. Cuando usted tiene los estados propios, usted también tiene los valores propios, y cuando se tiene los valores propios, puede resolver el…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo determinar estados propios osciladores armónicos de un sistema En la física cuántica, cuando tienes los estados propios de un sistema, se puede determinar los estados permitidos de sistema y la probabilidad relativa de que el sistema estará en cualquiera de esos estados.El conmutador de los operadores A, B…
¿Cómo encontrar los vectores propios y valores propios de un operador En la física cuántica, si te dan un operador en forma de matriz, usted puede encontrar sus vectores propios y valores propios. Por ejemplo, digamos que usted necesita para resolver la siguiente ecuación:En primer lugar, se puede reescribir esta…
¿Cómo encontrar el valor esperado de una tirada de dados Teniendo en cuenta que todo en la física cuántica se hace en términos de probabilidades, hacer predicciones es muy importante. Y el más grande tal predicción es el valor esperado. El valor esperado de un operador es el valor medio que usted…
¿Cómo encontrar la inversa de una matriz grande Encontrar la inversa de una matriz grande muchas veces no es fácil, por lo que los cálculos de física cuántica a veces se limita a trabajar con operadores unitarios, T, donde inversa del operador es igual a su adjunto,(Para encontrar el adjunto…
Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación…
Cómo utilizar los operadores para las cantidades de la física cuántica En la física cuántica, puede utilizar los operadores para ampliar las capacidades de sujetadores y mercados. A pesar de que han nombres que suena intimidante como Hamilton, la unidad, la pendiente, el momento lineal y Laplaciano, estos operadores…