Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico
Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación de resolver los problemas del oscilador armónico, ya que hacerlo es una forma inteligente de manejar la ecuación de Hamilton más dura. Esto es lo que estos dos operadores hacen:
Operador de la Creación. El operador de la creación eleva el nivel de energía de un estado propio de un nivel, por lo que si el oscilador armónico es en el cuarto nivel de energía, el operador de la creación eleva al quinto nivel.
Operador de aniquilación. El operador de la aniquilación hace lo contrario, la reducción de estados propios de una sola planta.
Estos operadores hacen que sea más fácil de resolver para el espectro de energía sin un montón de trabajo para la resolución de los estados propios reales. En otras palabras, se puede entender todo el espectro de energía mirando a la diferencia de energía entre los estados propios.
Así es como la gente suele resolver para el espectro de energía. En primer lugar, se introduce dos nuevos operadores, p y q, que se dimensionless- se refieren a la (impulso) operador P de esta manera:
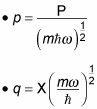
Utiliza estos dos nuevos operadores, p y q, como la base del operador de aniquilación, la, y el operador de la creación,
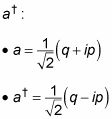
Ahora usted puede escribir el hamiltoniano oscilador armónico así, en términos de
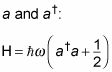
En cuanto a la creación de nuevos operadores aquí, los físicos cuánticos se volvió loca, incluso dando un nombre a
Así que aquí es cómo usted puede escribir el Hamilton:
El operador N devuelve el número del nivel de energía del oscilador armónico. Si denotan los estados propios de N como
recibe este, donde n es el número de la nº estado:
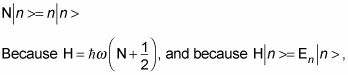
a continuación, mediante la comparación de las dos ecuaciones anteriores, usted tiene
Sorprendentemente, eso te da los valores propios de la energía de la nº estado de un oscilador armónico mecánica cuántica. Así que aquí están los estados de energía:
La energía del estado fundamental corresponde a n = 0:
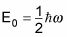
El primer estado excitado es
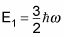
El segundo estado excitado tiene una energía de
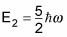
Etcétera. Es decir, los niveles de energía son discretos y no degenerada (no compartida por cualquiera de los dos estados). Por lo tanto, el espectro de energía se compone de bandas equidistantes.
Cómo organizar eingenvectors En la física cuántica, los vectores propios de un operador hermítica definen un conjunto completo de vectores ortonormales - es decir, una base completa para el espacio de estados. Cuando se ve en este " base propia, " que se construye de los…
Cómo crear estados propios del momento angular Puede crear los estados propios reales, | l, m>, de estados de momento angular en la mecánica cuántica. Cuando usted tiene los estados propios, usted también tiene los valores propios, y cuando se tiene los valores propios, puede resolver el…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo determinar estados propios osciladores armónicos de un sistema En la física cuántica, cuando tienes los estados propios de un sistema, se puede determinar los estados permitidos de sistema y la probabilidad relativa de que el sistema estará en cualquiera de esos estados.El conmutador de los operadores A, B…
¿Cómo encontrar cualquier estado excitado de un oscilador armónico Si puede determinar la función de onda para el estado fundamental de un oscilador armónico cuántico, entonces usted puede encontrar cualquier estado excitado de ese oscilador armónico.Por lo tanto, si usted sabe lo queparece, se puede determinar…
¿Cómo encontrar el nivel de energía de un oscilador armónico: un ejemplo Su instructor física cuántica puede pedirle que encontrar el nivel de energía de un oscilador armónico. La mejor manera de aprender es a través de un ejemplo. Digamos que usted tiene un protón someterse oscilación armónica concomo se muestra…
¿Cómo encontrar la energía de un oscilador cargada utilizando la teoría de la perturbación En la física cuántica, cuando se tiene los valores propios exactas para un oscilador cargada en un sistema perturbado, puede encontrar la energía del sistema. Basado en la teoría de la perturbación, la energía corregida del oscilador está…
¿Cómo encontrar el estado propio de energía de un oscilador armónico en el espacio posición En la física cuántica, puede utilizar los operadores para determinar el estado propio de energía de un oscilador armónico en el espacio posición. El encanto de la utilización de los operadores la yes que, dado el estado de la tierra, | 0>, los…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
Cómo utilizar los operadores para las cantidades de la física cuántica En la física cuántica, puede utilizar los operadores para ampliar las capacidades de sujetadores y mercados. A pesar de que han nombres que suena intimidante como Hamilton, la unidad, la pendiente, el momento lineal y Laplaciano, estos operadores…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Matrices de Pauli En la física cuántica, cuando se trabaja con estados propios de spin y operadores para partículas de espín 1/2 en términos de matrices, es posible que vea los operadores SX, Sy, y Sz escrito en términos de Pauli matrices,Teniendo en cuenta que…