Cómo crear estados propios del momento angular
Puede crear los estados propios reales, | l, m>, de estados de momento angular en la mecánica cuántica. Cuando usted tiene los estados propios, usted también tiene los valores propios, y cuando se tiene los valores propios, puede resolver el hamiltoniano y obtener los niveles de energía permitidos de un objeto con el momento angular.
No cometa el supuesto de que los estados propios son | l, m> - más bien, dicen que son
donde el valor propio de
Así que el valor propio de
Del mismo modo, el valor propio de
Para seguir adelante, tienes que introducir subir y bajar los operadores. De esa manera, usted puede resolver para el estado fundamental, por ejemplo, aplicando el operador de la reducción al estado fundamental y establecer el resultado igual a cero - y luego la solución para el estado fundamental en sí.
En este caso, el operador de fondos es L+ y el operador de la reducción es L-. Estos operadores suben y bajan el Lz número cuántico. Puede definir los operadores de subida y bajada de la siguiente manera:
Cría: L+ = LX + yoLy
Descenso: L- = LX - yoLy
Estas dos ecuaciones significan que
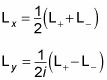
También puede ver que
Eso significa que los siguientes son todos iguales a L2:
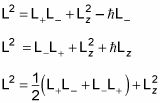
También puede ver que estas ecuaciones son verdaderas:
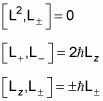
Bien, ahora usted puede poner todo esto funcione. Te estás volviendo a las cosas buenas.
Echa un vistazo a la operación de
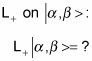
Ver qué
es, comenzar aplicando la Lz operador de esta manera:
De
puedes ver eso
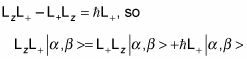
Y por eso
usted tiene lo siguiente:
Esta ecuación significa que la eigenstate
es también un estado propio del Lz operador, con un valor propio de
O de una manera más comprensible:
dónde c es una constante.
Así que la L+ operador tiene el efecto de elevar la
número cuántico en 1. Del mismo modo, el operador de la reducción hace esto:
Ahora echa un vistazo a lo que
es igual a:
Debido L2 es un escalar, se conmuta con todo. L2 L+ - L+ L2 = 0, por lo que esto es cierto:
Y por eso
usted tiene la siguiente ecuación:
Del mismo modo, el operador de bajada, L-, te da esto:
Así los resultados de estas ecuaciones significan que el
operadores no cambian el
en absoluto.
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo determinar estados propios osciladores armónicos de un sistema En la física cuántica, cuando tienes los estados propios de un sistema, se puede determinar los estados permitidos de sistema y la probabilidad relativa de que el sistema estará en cualquiera de esos estados.El conmutador de los operadores A, B…
¿Cómo encontrar valores propios del momento angular Cuando usted tiene los valores propios de estados de momento angular en la mecánica cuántica, puede resolver el hamiltoniano y obtener los niveles de energía permitidos de un objeto con el momento angular. Los valores propios del momento angular…
¿Cómo encontrar conmutadores de momento angular, l En la física cuántica, usted puede encontrar conmutadores de momento angular, L. Primera examinar LX, Ly, y yoz por echar un vistazo a la forma en que commute- si conmutan (por ejemplo, si [LX, Ly] = 0), entonces se puede medir cualquier dos de…
¿Cómo encontrar el estado propio de energía de un oscilador armónico en el espacio posición En la física cuántica, puede utilizar los operadores para determinar el estado propio de energía de un oscilador armónico en el espacio posición. El encanto de la utilización de los operadores la yes que, dado el estado de la tierra, | 0>, los…
¿Cómo encontrar los vectores propios y valores propios de un operador En la física cuántica, si te dan un operador en forma de matriz, usted puede encontrar sus vectores propios y valores propios. Por ejemplo, digamos que usted necesita para resolver la siguiente ecuación:En primer lugar, se puede reescribir esta…
¿Cómo encontrar el operador adjunto En la física cuántica, a menudo trabaja con adjoints hermitianas. los Operador adjunto - también llamado adjunto o Conjugado hermítica - de un operador A se denotaPara encontrar el operador adjunto, sigue estos pasos:Reemplazar constantes…
¿Cómo encontrar la inversa de una matriz grande Encontrar la inversa de una matriz grande muchas veces no es fácil, por lo que los cálculos de física cuántica a veces se limita a trabajar con operadores unitarios, T, donde inversa del operador es igual a su adjunto,(Para encontrar el adjunto…
Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación…
Cómo utilizar los operadores para las cantidades de la física cuántica En la física cuántica, puede utilizar los operadores para ampliar las capacidades de sujetadores y mercados. A pesar de que han nombres que suena intimidante como Hamilton, la unidad, la pendiente, el momento lineal y Laplaciano, estos operadores…
¿Cómo trabajar con vectores propios y eingenvalues En la física cuántica, al trabajar con mercados, es útil saber cómo utilizar vectores propios y valores propios. La aplicación de un operador a un ket puede dar lugar a una nueva ket:Para facilitar las cosas, se puede trabajar con vectores…
Matrices de Pauli En la física cuántica, cuando se trabaja con estados propios de spin y operadores para partículas de espín 1/2 en términos de matrices, es posible que vea los operadores SX, Sy, y Sz escrito en términos de Pauli matrices,Teniendo en cuenta que…