¿Cómo trabajar con vectores propios y eingenvalues
En la física cuántica, al trabajar con mercados, es útil saber cómo utilizar vectores propios y valores propios. La aplicación de un operador a un ket puede dar lugar a una nueva ket:
Para facilitar las cosas, se puede trabajar con vectores propios y valores propios (eigen es alemana para " innata " o " natural "). Por ejemplo,
es un vector propio de A si el operador
El numero la es una constante compleja
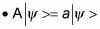
Nota lo que pasa aquí: Aplicación de la A a uno de sus vectores propios,
multiplicado por el vector propio de valor propio, la.
A pesar de que la puede ser una constante compleja, los valores propios de los operadores hermitianos son números reales, y sus vectores propios son ortogonales
Lanzamiento de un problema en términos de vectores propios y valores propios puede hacer la vida mucho más fácil, ya aplicar el operador a sus vectores propios simplemente te da el mismo vector propio de nuevo, multiplicado por su valor propio - no hay cambio molestos de Estado, por lo que no tiene que tratar con un vector de estado diferente.
Echa un vistazo a esta idea, usando el operador R ruede los dados, que se expresa de esta manera en forma matricial:
El operador R funciona en el espacio de 11 dimensiones y es hermitiana, por lo que habrá 11 vectores propios ortogonales y 11 correspondientes valores propios.
Debido a que R es una matriz diagonal, encontrar los vectores propios es fácil. Usted puede tomar vectores unitarios en las 11 direcciones diferentes como los vectores propios. Esto es lo que el primer vector propio,
se vería así:
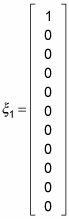
Y esto es lo que el segundo vector propio,
se vería así:
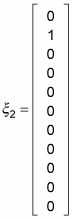
Y así sucesivamente, hasta
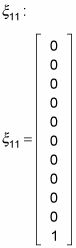
Tenga en cuenta que todos los vectores propios son ortogonales.
Y los valores propios? Son los números que se obtienen cuando se aplica el operador R para un vector propio. Debido a que los vectores propios son vectores unitarios sólo en los 11 dimensiones, los valores propios son los números de la diagonal de la matriz R: 2, 3, 4, y así sucesivamente, hasta 12.
Cómo nombrar a los valores de sus vectores en r A menudo, los elementos de vectores se denominan por sus posiciones - es decir, x [5] se refiere a la quinta elemento en el vector X. Una característica muy potente en I, sin embargo, da nombres a los elementos de un vector, que le permite…
Cómo realizar varios cálculos con vectores utilizando r R es un lenguaje basado en vectores. Usted puede pensar en un vector como una fila o columna de números o texto. La lista de números {1,2,3,4,5}, por ejemplo, podría ser un vector. A diferencia de la mayoría de otros lenguajes de programación,…
Cómo utilizar vectores lógicos como índices en r La función de índice en I no toma sólo vectores numéricos como arguments- también trabaja con vectores lógicos. Puede utilizar estos vectores lógicos de manera muy eficiente para seleccionar algunos valores de un vector.Si utiliza un vector…
Adición y sustracción de vectores Puede sumar y restar vectores en un gráfico al comenzar un vector en el punto final de otro vector. Sumar y restar vectores de componente a componente, de la siguiente manera:Al agregar o restar dos vectores, el resultado es un…
Cálculo de magnitud con vectores Los vectores se utilizan comúnmente para modelar las fuerzas como el viento, las corrientes marinas, la gravedad y el electromagnetismo. Cálculo de la magnitud de los vectores es esencial para todo tipo de problemas donde las fuerzas…
Cómo construir vectores en r LA vector es el tipo más simple de estructura de datos en el manual de R. El R define un vector como se " una sola entidad que consiste en una colección de cosas ". Una colección de números, por ejemplo, es un vector numérico - los primeros…
Cómo crear vectores en r Para crear un vector de una simple secuencia de números enteros, por ejemplo, se utiliza el operador coma (:) En R. El código de 3: 7 le da un vector con los números 3 a 7, y 4: -3 crea un vector con los números 4 a -3, tanto en pasos de 1.Para…
Cálculo del vector resultante de dos vectores de desplazamiento En la física, al igual que usted puede agregar dos números para obtener un tercer número, puede añadir dos vectores de obtener un resultante vector. Para demostrar que va a añadir dos vectores, puso las flechas juntos para que se parte de…
Cómo agregar vectores en una cuadrícula Puede utilizar los componentes de vectores para agregar vectores juntos utilizando una cuadrícula. Si lo hace, reduce el problema de la adición de vectores a una simple combinación de la adición de números juntos, lo cual es muy útil cuando a…
Cómo organizar eingenvectors En la física cuántica, los vectores propios de un operador hermítica definen un conjunto completo de vectores ortonormales - es decir, una base completa para el espacio de estados. Cuando se ve en este " base propia, " que se construye de los…
¿Cómo encontrar los valores propios y vectores propios para hamiltonianos degenerados El uso de la física cuántica, se puede determinar la F valores y vectores propios coincidencia para sistemas en los que las energías son degenerados. Echa un vistazo a este hamiltoniano no perturbado:En otras palabras, varios estados tienen la…
¿Cómo encontrar los vectores propios y valores propios de un operador En la física cuántica, si te dan un operador en forma de matriz, usted puede encontrar sus vectores propios y valores propios. Por ejemplo, digamos que usted necesita para resolver la siguiente ecuación:En primer lugar, se puede reescribir esta…