¿Cómo encontrar los valores propios y vectores propios para hamiltonianos degenerados
El uso de la física cuántica, se puede determinar la F valores y vectores propios coincidencia para sistemas en los que las energías son degenerados. Echa un vistazo a este hamiltoniano no perturbado:
En otras palabras, varios estados tienen la misma energía. Dicen los estados de energía son F-veces degenerada, como este:
¿Cómo afecta esto a la imagen de perturbación? El hamiltoniano completa, H, se compone de la, hamiltoniano no perturbado original, H0, y el hamiltoniano perturbación,
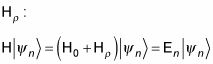
En orden cero aproximación, se puede escribir la función propia
como una combinación de los estados degenerados
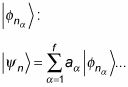
Cabe destacar que en lo que sigue, se supone que
si m no es igual a n. Además, se asume que el
están normalizados - es decir,
Al conectar esta ecuación de orden cero en la ecuación de Hamilton completa, se obtiene
Ahora multiplicando la ecuación por
te dio
Usando el hecho de que
si m no es igual a n te dio
Los físicos suelen escribir la ecuación como
dónde
Y la gente también escriben que la ecuación como
donde E(1)n = En - E(0)n. Eso es un sistema de ecuaciones lineales, y existe la solución sólo cuando el determinante de esta matriz es no nula:
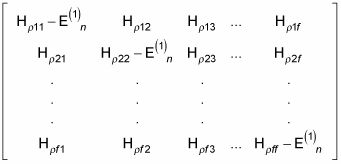
El determinante de esta matriz es una Fecuación de grado º en E(1)n, y tiene F diferentes raíces,
Aquellas F diferentes raíces son las correcciones de primer orden para el hamiltoniano. Por lo general, esas raíces son diferentes debido a la perturbación aplicada. En otras palabras, la perturbación normalmente se deshace de la degeneración.
Así que aquí está el camino a encontrar los valores propios a la primera orden - se configura una F-por casoF matriz del hamiltoniano perturbación,
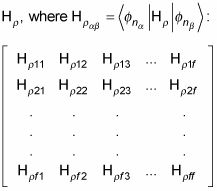
Entonces diagonalizar esta matriz y determinar la F valores propios
y los vectores propios que coinciden:
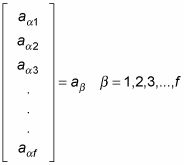
Entonces usted consigue los valores propios de la energía a primer orden de esta manera:
Y son los vectores propios
-
Cómo escribir un sistema en forma de matriz -
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden -
Deducir la fórmula para la energía de rotación de una molécula diatómica -
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro -
Cómo organizar eingenvectors -
Cómo crear estados propios del momento angular
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo determinar estados propios osciladores armónicos de un sistema En la física cuántica, cuando tienes los estados propios de un sistema, se puede determinar los estados permitidos de sistema y la probabilidad relativa de que el sistema estará en cualquiera de esos estados.El conmutador de los operadores A, B…
¿Cómo encontrar valores propios del momento angular Cuando usted tiene los valores propios de estados de momento angular en la mecánica cuántica, puede resolver el hamiltoniano y obtener los niveles de energía permitidos de un objeto con el momento angular. Los valores propios del momento angular…
¿Cómo encontrar la energía de un oscilador cargada utilizando la teoría de la perturbación En la física cuántica, cuando se tiene los valores propios exactas para un oscilador cargada en un sistema perturbado, puede encontrar la energía del sistema. Basado en la teoría de la perturbación, la energía corregida del oscilador está…
¿Cómo encontrar los vectores propios y valores propios de un operador En la física cuántica, si te dan un operador en forma de matriz, usted puede encontrar sus vectores propios y valores propios. Por ejemplo, digamos que usted necesita para resolver la siguiente ecuación:En primer lugar, se puede reescribir esta…
¿Cómo encontrar las correcciones de primer orden a los niveles de energía y funciones de onda En la física cuántica, con el fin de encontrar las correcciones de primer orden a los niveles de energía y funciones de onda de un sistema perturbado, En, es necesario calcular E(1)n, al igual queAsique como haces eso? Usted comienza con tres…
¿Cómo encontrar las correcciones de segundo orden a los niveles de energía y funciones de onda En la física cuántica, con el fin de encontrar las correcciones de segundo orden a los niveles de energía y funciones de onda de un sistema perturbado, En, es necesario calcular E(2)n, al igual queAsique como haces eso? Usted comienza con tres…
¿Cómo encontrar la energía total de un sistema de múltiples partículas El hamiltoniano representa la energía total de todas las partículas en un sistema multi-partícula. Puede describir ese sistema en términos de la física cuántica. La siguiente figura muestra un sistema de múltiples partículas donde un número…
Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación…
¿Cómo trabajar con vectores propios y eingenvalues En la física cuántica, al trabajar con mercados, es útil saber cómo utilizar vectores propios y valores propios. La aplicación de un operador a un ket puede dar lugar a una nueva ket:Para facilitar las cosas, se puede trabajar con vectores…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica y el hamiltoniano Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…