Deducir la fórmula para la energía de rotación de una molécula diatómica
categoría Educación y lenguas / Ciencia / Física
He aquí un ejemplo que implica encontrar el espectro de energía de rotación de una molécula diatómica. La figura muestra la configuración: Una molécula diatómica rotación se compone de dos átomos con las masas m1 y m2. La primera átomo gira a r = r1, y el segundo átomo de gira a r = r2. ¿Cuál es la energía de rotación de la molécula?
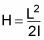
Una molécula diatómica giratorio.
El hamiltoniano es
I es el momento de inercia de rotación, que es
dónde r = |r1 - r2| y
Porque
Por lo tanto, el hamiltoniano se convierte en
Así que aplicando el hamiltoniano de los estados propios, | l, m >, Le da la siguiente:
Y como usted sabe,
por lo que esta ecuación se convierte
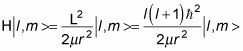
Y debido H | l, m > = E | l, m >, Se puede ver que
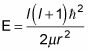
Y esa es la energía en función de l, el número cuántico del momento angular.




