Cómo calcular la degeneración de energía de un átomo de hidrógeno en términos de n, l, m y
Cada estado cuántico del átomo de hidrógeno se especifica con tres números cuánticos: n (el número cuántico principal), l (el número cuántico del momento angular del electrón), y m (el z componente del momento angular del electrón,
¿Cuántos de estos estados tienen la misma energía? En otras palabras, ¿cuál es la degeneración de energía del átomo de hidrógeno en términos de los números cuánticos n, l, y m?
Bueno, la energía real depende sólo en n, como se ve en la siguiente ecuación:
Eso significa que el E es independiente de l y m. Entonces, ¿cuántos estados, |n, l, m>, Tienen la misma energía para un valor particular de n? Bueno, para un valor particular de n, l puede variar desde cero hasta n - 1. Y cada l puede tener diferentes valores de m, por lo que la degeneración total es
La degeneración en m es el número de estados con diferentes valores de m que tienen el mismo valor de l. Para cualquier valor particular de l, puedes tener m valores de -l, -l + 1, ..., 0, ..., l - 1, l. Y eso es (2l + 1) posible m Unidos por un valor particular de l. Así que usted puede conectar (2l + 1) por la degeneración en m:
Y esta serie resulta ser simplemente n2.
Así que la degeneración de los niveles de energía del átomo de hidrógeno es n2. Por ejemplo, el estado fundamental, n = 1, tiene degeneración = n2 = 1 (que tiene sentido porque l, y por lo tanto m, sólo puede ser igual a cero para este estado).
por n = 2, usted tiene una degeneración 4:
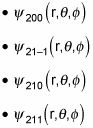
Guay.
Reglas para la asignación de los números de oxidación de los elementos Los números de oxidación son números contables. Permiten que los químicos que se pueden hacer cosas como el equilibrio redox (rojoucción /bueydación) ecuaciones. Los números de oxidación son números positivos o negativos, pero no los…
Elementos científicos y electrónica Un elemento es un tipo de átomo, que se define por el número de protones en su núcleo. Cobre - un elemento que es importante en la electrónica - tiene 29 protones en su núcleo. Por otro lado, los átomos de hidrógeno tienen un solo protón en…
Calcular la distancia de un electrón desde el protón de un átomo de hidrógeno Cuando usted quiere encontrar en un electrón es en un momento dado en un átomo de hidrógeno, lo que en realidad estás haciendo es encontrar en qué medida el electrón es del protón. Usted puede encontrar el valor esperado de r, eso es, , para…
Deducir la fórmula para la energía de rotación de una molécula diatómica He aquí un ejemplo que implica encontrar el espectro de energía de rotación de una molécula diatómica. La figura muestra la configuración: Una molécula diatómica rotación se compone de dos átomos con las masas m1 y m2. La primera átomo…
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno Usando la ecuación # 246-dinger Schröder dice que casi todo lo que necesitas saber sobre el átomo de hidrógeno, y todo se basa en una sola hipótesis: que la función de onda debe ir a cero r va hasta el infinito, que es lo que hace que la…
Encuentra el punto que falta con el experimento de Stern-Gerlach El experimento de Stern-Gerlach reveló inesperadamente la existencia de la vuelta atrás en el 1922. Los físicos Otto Stern y Walther Gerlach envió un haz de átomos de plata a través de los polos de un imán - cuyo campo magnético estaba en el…
Cómo calcular el espín de un electrón en un átomo de hidrógeno Al calcular el espín de un electrón en un átomo de hidrógeno, es necesario para permitir el giro del electrón, que proporciona estados cuánticos adicionales. Dada la siguiente ecuación, donde la función de onda del átomo de hidrógeno es un…
Cómo crear estados propios del momento angular Puede crear los estados propios reales, | l, m>, de estados de momento angular en la mecánica cuántica. Cuando usted tiene los estados propios, usted también tiene los valores propios, y cuando se tiene los valores propios, puede resolver el…
Cómo determinar las energías permitidas de un átomo de hidrógeno Cuando se aplica el Schr # 246-dinger ecuación mecánica cuántica para un átomo de hidrógeno, la condición de cuantificación para la función de onda r para permanecer como finito r# 32 va al infinito esdóndeSustituyendoen la ecuación de…
¿Cómo encontrar valores propios del momento angular Cuando usted tiene los valores propios de estados de momento angular en la mecánica cuántica, puede resolver el hamiltoniano y obtener los niveles de energía permitidos de un objeto con el momento angular. Los valores propios del momento angular…
¿Cómo encontrar los niveles de energía cuadrados así En la física cuántica, no sé si las condiciones de contorno de un cuadrado bien, usted puede encontrar theenergy niveles de un electrón.La ecuacionle dice que usted tiene que utilizar las condiciones de contorno para encontrar las constantes A y…
¿Cómo mantener una función de r finito cuando r tiende a infinito En la física cuántica, la hora de encontrar la solución para una ecuación radial para un átomo de hidrógeno, que necesita para mantener la función de r finito como r tiende a infinito para evitar que la solución se vuelva no físico. Usted…