¿Cómo encontrar valores propios del momento angular
Cuando usted tiene los valores propios de estados de momento angular en la mecánica cuántica, puede resolver el hamiltoniano y obtener los niveles de energía permitidos de un objeto con el momento angular. Los valores propios del momento angular son los valores posibles del momento angular puede tomar.
Aquí es cómo derivar ecuaciones con estado propio
Tenga en cuenta que L2 - Lz2 = LX2 + Ly2, que es un número positivo, por lo
Eso significa que
Y sustituyendo en
y utilizando el hecho de que los estados propios se normalizan, le da esta:
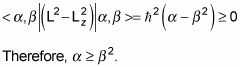
Así que hay un valor máximo posible de
que se puede llamar
Puede ser inteligente ahora, porque tiene que haber un estado
de tal manera que no se puede plantear
nunca más. Por lo tanto, si se aplica el operador de fondos, se obtiene cero:
Aplicando el operador bajar a este también le da cero:
Y por eso
eso significa que el siguiente es cierto:
Poner en
te da esto:
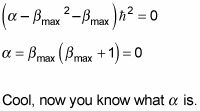
En este punto, es habitual cambiar de nombre
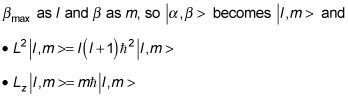
Se puede decir aún más. Además de una
también debe haber un
de tal manera que cuando se aplica el operador bajar, L-, se obtiene cero, porque no se puede ir a cualquier menor que
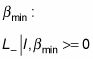
Y usted puede aplicar L+ en esto también:
De
tu sabes
que se da la siguiente:
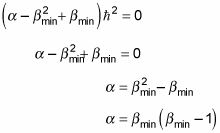
Y comparando esta ecuación para
te dio
Tenga en cuenta que debido a que llegue
por n aplicaciones sucesivas de
se obtiene el siguiente:
El acoplamiento de estas dos ecuaciones le da
Por Consiguiente,
puede ser un número entero o un número entero media (dependiendo de si n es par o impar).
Porque
y n es un número positivo, puede encontrar que
Así que ahora lo tienen:
Los estados propios son | l, m >.
El número cuántico del momento angular total es l.
El número cuántico del momento angular a lo largo del z eje es m.
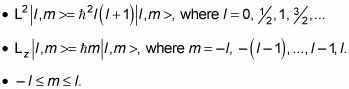
Para cada l, hay 2l + 1 Valores de m. Por ejemplo, si l = 2, entonces m puede ser igual a -2, -1, 0, 1, o 2.
Usted puede ver una L representativa y Lz en la figura.
L es el momento angular total y Lz es la proyección de ese momento angular total en el z eje.
Encuentra el punto que falta con el experimento de Stern-Gerlach El experimento de Stern-Gerlach reveló inesperadamente la existencia de la vuelta atrás en el 1922. Los físicos Otto Stern y Walther Gerlach envió un haz de átomos de plata a través de los polos de un imán - cuyo campo magnético estaba en el…
Encuentra los valores propios de la subida y bajada operadores del momento angular En la física cuántica, se pueden encontrar los valores propios de la elevación y descenso operadores del momento angular, que subir y bajar un estado de z componente del momento angular.Empieza por tomar un vistazo a L+, y un plan para resolver…
Cómo angular obras de aceleración Si los puntos de velocidad de vector angular fuera del plano de rotación de una rueda, puede usar la física para determinar lo que sucede cuando los cambios de velocidad angular - cuando la rueda se acelera o ralentiza. Un cambio en la velocidad…
Cómo operadores de spin se asemejan a los operadores del momento angular Debido giro es un tipo de momento angular incorporado, operadores de spin tienen mucho en común con los operadores de momento angular orbital. A medida que su instructor de la física cuántica le dirá, hay operadores de spin análogas, S2 y Sz,…
Cómo calcular el momento angular En física, se puede calcular el momento angular de la misma manera que se calcula la cantidad de movimiento - sólo momento sustituto de inercia de la masa, y la velocidad angular de la velocidad.Imagínate a un niño pequeño en un paseo patio…
Cómo calcular la frecuencia angular de una masa en un resorte En física, se puede aplicar la ley de Hooke, junto con el concepto de movimiento armónico simple, para encontrar la frecuencia angular de una masa en un resorte. Y debido a que se puede relacionar la frecuencia angular y la masa en la primavera,…
Cómo calcular la degeneración de energía de un átomo de hidrógeno en términos de n, l, m y Cada estado cuántico del átomo de hidrógeno se especifica con tres números cuánticos: n (el número cuántico principal), l (el número cuántico del momento angular del electrón), y m (el z componente del momento angular del…
Cómo calcular el par necesario para acelerar un disco giratorio Puede usar la física para calcular la cantidad de par necesario para acelerar (o desacelerar) la velocidad de un disco giratorio. Sin la capacidad de cambiar la velocidad de un disco, sería imposible para que usted pueda ver una película en el…
¿Cómo cambiar las ecuaciones de movimiento lineal para el movimiento de rotación En la física, cuando se pasa de un movimiento lineal a un movimiento de rotación, es necesario cambiar las ecuaciones que se utilizan para calcular los resultados. Aquí están los equivalentes angulares (o análogos) para las ecuaciones de…
¿Cómo cambiar las coordenadas rectangulares a coordenadas esféricas En la física cuántica, para encontrar las funciones propias reales (no sólo los estados propios) de los operadores de momento angular como L2 y yoz, te apartas de coordenadas rectangulares, X, y, y z, a coordenadas esféricas, ya que va a hacer…
Cómo crear estados propios del momento angular Puede crear los estados propios reales, | l, m>, de estados de momento angular en la mecánica cuántica. Cuando usted tiene los estados propios, usted también tiene los valores propios, y cuando se tiene los valores propios, puede resolver el…
Cómo determinar la dirección de la velocidad angular En la física, cuando una rueda está girando, no sólo tiene una velocidad angular, sino también una dirección. Esto es lo que el vector velocidad angular le dice:El tamaño del vector velocidad angular le indica la velocidad angular.La…