¿Cómo cambiar las coordenadas rectangulares a coordenadas esféricas
En la física cuántica, para encontrar las funciones propias reales (no sólo los estados propios) de los operadores de momento angular como L2 y yoz, te apartas de coordenadas rectangulares, X, y, y z, a coordenadas esféricas, ya que va a hacer los cálculos mucho más simple (después de todo, el momento angular es acerca de las cosas que van en círculos). La siguiente figura muestra el sistema de coordenadas esféricas.
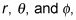
En el sistema rectangular (cartesiana) de coordenadas, se utiliza X, y, y z para orientarse. En el sistema de coordenadas esféricas, también usa tres cantidades:
como muestra la figura. Usted puede traducir entre el sistema de coordenadas esféricas y la rectangular de esta manera: El r vector es longitud del vector a la partícula que tiene momento angular,
es el ángulo de r desde el z eje, y
es el ángulo de r desde el X eje.
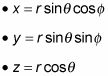
Considere las ecuaciones de momento angular:
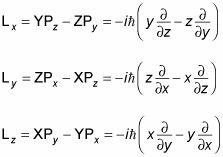
Cuando usted toma las ecuaciones de momento angular con las ecuaciones de conversión de sistema de coordenadas esféricas, se puede derivar la siguiente:
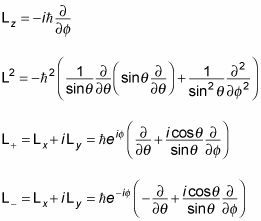
Bueno, estas ecuaciones se ven bastante involucrados. Pero hay una cosa a notar: Dependen únicamente en
lo que significa que sus estados propios dependen sólo de
no en r. Así las funciones propias de los operadores en la lista anterior pueden ser denotados como esto:
Tradicionalmente, le das el nombre
a las funciones propias del momento angular en coordenadas esféricas, por lo que tiene lo siguiente:
Muy bien, es hora de trabajar en la búsqueda de la forma real de
Usted sabe que cuando se utiliza la L2 y yoz operadores en estados propios del momento angular, se obtiene lo siguiente:
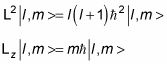
Así que lo siguiente debe ser verdad:
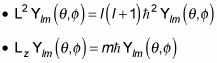
De hecho, se puede ir más allá. Tenga en cuenta que Lz depende sólo de
lo que sugiere que se puede dividir
arriba en una parte que depende de
y una parte que depende de
Splitting
en partes tiene este aspecto:
Eso es lo que hace que trabajar con coordenadas esféricas tan útil - se puede dividir las funciones propias en dos partes, una que depende sólo de
y una parte que depende sólo de
Cómo calcular funciones trigonométricas usando cualquier círculo Cuando la determinación de los valores de la función trigonométrica de ángulos graficadas en la posición estándar en un círculo cuyo centro está en el origen, usted no tiene que tener un círculo unitario para calcular coordenadas. Puede…
Aplicando la ecuación schr & # 246-dinger en tres dimensiones En la física cuántica, se puede aplicar el Schr # 246-dinger ecuación cuando se trabaja en los problemas que tienen un potencial central. Estos son problemas donde usted es capaz de separar la función de onda en una parte radial (que depende de…
La aplicación de las funciones de Bessel y Neumann esféricas para una partícula libre En la física cuántica, puede aplicar las funciones esféricas de Bessel y Neumann para una partícula libre (una partícula que no está limitado por ningún potencial). La función de onda en coordenadas esféricas toma esta forma:yle da los…
La determinación de la parte angular de una función de onda En la física cuántica, se puede determinar la parte angular de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte…
La determinación de la parte radial de una función de onda En la física cuántica, se puede determinar la parte radial de una función de onda cuando se trabaja en los problemas que tienen un potencial central. Con problemas potenciales centrales, usted es capaz de separar la función de onda en una parte…
Encuentra las funciones propias de lz en coordenadas esféricas En algún momento, su instructor física cuántica puede pedirle que encontrar las funciones propias de la Lz en coordenadas esféricas. En coordenadas esféricas, la Lz operador tiene este aspecto:que es la siguiente:Y por esoesta ecuación se…
Cómo operadores de spin se asemejan a los operadores del momento angular Debido giro es un tipo de momento angular incorporado, operadores de spin tienen mucho en común con los operadores de momento angular orbital. A medida que su instructor de la física cuántica le dirá, hay operadores de spin análogas, S2 y Sz,…
Cómo agregar vectores juntos Se le pide con frecuencia para añadir vectores en la resolución de problemas de física. Para sumar dos vectores, se colocan la cabeza a la cola y luego encontrar la duración y magnitud del resultado. El orden en que se agregan los dos vectores…
Cómo crear estados propios del momento angular Puede crear los estados propios reales, | l, m>, de estados de momento angular en la mecánica cuántica. Cuando usted tiene los estados propios, usted también tiene los valores propios, y cuando se tiene los valores propios, puede resolver el…
¿Cómo encontrar valores propios del momento angular Cuando usted tiene los valores propios de estados de momento angular en la mecánica cuántica, puede resolver el hamiltoniano y obtener los niveles de energía permitidos de un objeto con el momento angular. Los valores propios del momento angular…
¿Cómo encontrar componentes de un vector Puede convertir de la manera magnitud / ángulo de la especificación de un vector para la forma de coordenadas de expresión. Si lo hace, es esencial para los tipos de operaciones que puede esperar para ejecutar en vectores, tales como cuando se…
¿Cómo encontrar conmutadores de momento angular, l En la física cuántica, usted puede encontrar conmutadores de momento angular, L. Primera examinar LX, Ly, y yoz por echar un vistazo a la forma en que commute- si conmutan (por ejemplo, si [LX, Ly] = 0), entonces se puede medir cualquier dos de…