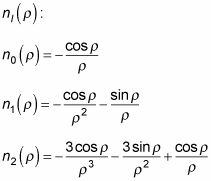La aplicación de las funciones de Bessel y Neumann esféricas para una partícula libre
En la física cuántica, puede aplicar las funciones esféricas de Bessel y Neumann para una partícula libre (una partícula que no está limitado por ningún potencial). La función de onda en coordenadas esféricas toma esta forma:
y
le da los armónicos esféricos. El problema es ahora para resolver para la parte radial, Rnl(r). Aquí está la ecuación radial:
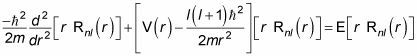
Para una partícula libre, V (r) = 0, por lo que la ecuación radial se convierte
La forma en que usualmente maneja esta ecuación es sustituir
y porque tiene una versión de la misma ecuación para cada n índice es conveniente simplemente eliminarlo, por lo que Rnl (r) Se convierte
Esta sustitución significa que
se convierte en la siguiente:
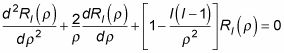
La parte radial de la ecuación parece difícil, pero las soluciones llegar a ser bien conocido - esta ecuación se llama la ecuación de Bessel esférica, y la solución es una combinación de las funciones de Bessel esféricas
y las funciones esféricas Neumann
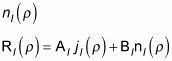
donde unl y Bl son constantes. ¿Cuáles son las funciones esféricas de Bessel y las funciones esféricas Neumann? Las funciones de Bessel esféricas están dadas por
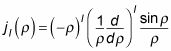
Esto es lo que las primeras iteraciones de
parece:
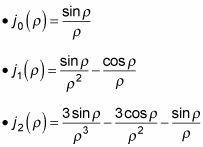
¿Qué hay de las funciones esféricas Neumann? Las funciones esféricas Neumann están dadas por
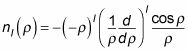
Aquí están las primeras iteraciones de
-
Cómo trazar coordenadas esféricas -
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
Aplicando la ecuación radial en el interior del pozo cuadrado -
La determinación de la parte radial de una función de onda -
Encontrar los límites de rho pequeños y grandes de una partícula libre
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer a encontrar la ecuación de energía total para los problemas de partículas libres tridimensionales. La energía total de la partícula libre es la suma de la energía en tres…
Encuentra las funciones propias de lz en coordenadas esféricas En algún momento, su instructor física cuántica puede pedirle que encontrar las funciones propias de la Lz en coordenadas esféricas. En coordenadas esféricas, la Lz operador tiene este aspecto:que es la siguiente:Y por esoesta ecuación se…
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
¿Cómo cambiar las coordenadas rectangulares a coordenadas esféricas En la física cuántica, para encontrar las funciones propias reales (no sólo los estados propios) de los operadores de momento angular como L2 y yoz, te apartas de coordenadas rectangulares, X, y, y z, a coordenadas esféricas, ya que va a hacer…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar las funciones propias de l2 en coordenadas esféricas Su instructor física cuántica puede pedirle que encontrar las funciones propias de la L2 en coordenadas esféricas. Para ello, se comienza con la función propia deldado que en coordenadas esféricas, la L2 operador tiene este aspecto:Eso es todo…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…