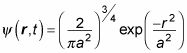Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones
En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución para
si se recuerda que, para una partícula libre,
Esa ecuación que da esta forma de
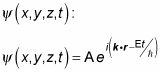
Porque
la ecuación se convierte en
De hecho, ahora que el lado derecho de la ecuación es en términos del radio vector r, usted puede hacer el partido del lado izquierdo:
Esa es la solución a la Schr # 246-dinger ecuación, pero es no físico. ¿Por qué? Tratando de normalizar esta ecuación en tres dimensiones, por ejemplo, se da la siguiente, donde A es una constante:
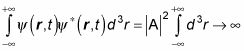
(Recuerde que el símbolo del asterisco
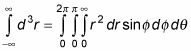
Por lo tanto, los integral diverge y usted no puede normalizar
como escrito aquí. Entonces, ¿qué hace usted aquí para obtener una partícula física?
La clave para resolver este problema es darse cuenta de que si usted tiene una serie de soluciones a la Schr # 246-dinger ecuación, entonces cualquier combinación lineal de estas soluciones es también una solución. En otras palabras, se agregan varias funciones de onda en conjunto de manera que se obtiene una paquete de ondas, que es una colección de funciones de onda de la forma
de tal manera que
Las funciones de onda interfieren constructivamente en una ubicación.
Interfieren destructiva (ir a cero) en todos los demás lugares.
Mira la versión independiente del tiempo:
Sin embargo, para una partícula libre, los estados de energía no están separados en distintas bandas- las posibles energías son continuas, por lo que la gente escribe esta suma como una integral:
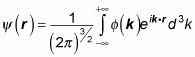
Entonces, ¿qué es
Es el análogo tridimensional de
Es decir, es la amplitud de cada función de onda componente. Puede encontrar
a partir de la transformada de Fourier
Me gusta esto:
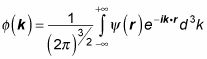
En la práctica, usted elige
tú mismo. Mira un ejemplo, utilizando el siguiente formulario para
que es para un paquete de ondas gaussiano (Nota: La parte exponencial es lo que hace de esta una forma de onda de Gauss):
dónde la y A son constantes. Usted puede comenzar por la normalización
para determinar que A es. He aquí cómo funciona:
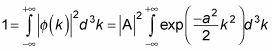
Bueno. Realización de la integral que da
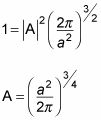
lo que significa que la función de onda es
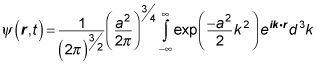
Usted puede evaluar esta ecuación para darle el siguiente, que es lo que la función de onda independiente del tiempo para un paquete de ondas gaussiano se ve como en 3D:
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Aplicando la ecuación radial fuera de la plaza, así -
La determinación de la parte radial de una función de onda -
Encontrar los límites de rho pequeños y grandes de una partícula libre -
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar la función de onda normalizada para una partícula en una plaza así infinito En la física cuántica, si se le da la ecuación de onda para una partícula en un pozo cuadrado infinito, se le puede pedir a normalizar la función de onda. Por ejemplo, comenzar con la siguiente ecuación de onda:La función de onda es una onda…
Cómo relacionar la amplitud de dispersión y la sección transversal diferencial de partículas spinless La amplitud de dispersión de partículas spinless es crucial para la comprensión de dispersión desde el punto de vista de la física cuántica. Para ver esto, eche un vistazo a las densidades de corriente, Jinc (la densidad de flujo de una…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…