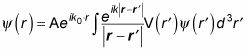Cómo relacionar la amplitud de dispersión y la sección transversal diferencial de partículas spinless
La amplitud de dispersión de partículas spinless es crucial para la comprensión de dispersión desde el punto de vista de la física cuántica. Para ver esto, eche un vistazo a las densidades de corriente, Jinc (la densidad de flujo de una partícula incidente dado) y Jsc (la densidad de corriente para una partícula dispersa dado):
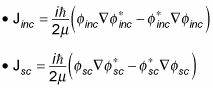
(Recuerde que el símbolo del asterisco
Inserción de sus expresiones para
en estas ecuaciones le da la siguiente, donde
es la amplitud de dispersión:
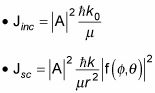
Ahora bien, en términos de la densidad de corriente, el número de partículas
dispersos en
y que pasa por un área
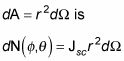
Enchufar
en la ecuación anterior le da
También, recordar que
Usted obtiene
Y aquí está el truco - para la dispersión elástica, k = k0, lo que significa que esta es su resultado final:
El problema de la determinación de la sección transversal diferencial se descompone para la determinación de la amplitud de dispersión.
Para encontrar la amplitud de dispersión - y por lo tanto la sección transversal diferencial - de partículas spinless, se trabaja en la solución del Schr # 246-dinger ecuación:
También puede escribir esto como
Usted puede expresar la solución a esa ecuación diferencial como la suma de una solución homogénea y una solución particular:
La solución homogénea satisface esta ecuación:
Y la solución homogénea es una onda plana - es decir, que corresponde a la onda plana incidente:
Para echar un vistazo a la dispersión que ocurre, usted tiene que encontrar la solución particular. Usted puede hacer eso en términos de funciones de Green, por lo que la solución a
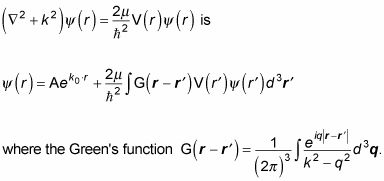
Esta integral se descompone al
Puede resolver la ecuación anterior en términos de ondas entrantes y / o salientes. Debido a que la partícula dispersada es una onda de salida, la función de Green toma esta forma:
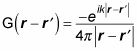
Usted ya sabe que
Así que la sustitución
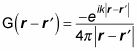
en la ecuación anterior le da
-
Ecuaciones diferenciales libro para los maniquíes - ¿Cómo decirle a una ecuación diferencial de otro
-
Comprobación de soluciones de ecuaciones diferenciales -
Definición de ecuaciones diferenciales homogéneas y no homogéneas -
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden -
Encuentra las funciones propias de lz en coordenadas esféricas
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo En la física cuántica, se puede utilizar el Schr # 246-dinger ecuación para ver cómo la función de onda de una partícula en un pozo cuadrado infinito evoluciona con el tiempo. El Schr # 246-dinger ecuación es la siguiente:También puede…
Cómo física cuántica convierte el impulso y la posición en probabilidades La física cuántica, a diferencia de la física clásica, es completamente determinista. Nunca se puede saber la preciso posición y el momento de una partícula en un momento dado. Usted puede dar sólo probabilidades para estas mediciones…
Cómo el efecto Compton de la luz explica desplazamiento de longitud de onda Aunque Max Planck y Albert Einstein postuló que la luz podía comportarse como tanto una onda y una partícula, fue Arthur Compton quien finalmente demostró que esto era posible. Su experimento involucró esparciendo fotones de electrones, como la…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
Cómo obtener las funciones de onda incidente y dispersos de partículas spinless Desde un punto de la física cuántica independiente del tiempo de vista, se puede derivar la onda incidente y funciones de onda dispersos de dos partículas no relativistas spinless. Para ello, es necesario asumir que la interacción entre las…
Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
¿Cómo traducir secciones transversales entre el centro de masa y los marcos de laboratorio En la física cuántica, una vez que usted se relaciona los ángulos de las partículas dispersas en el marco del laboratorio y el centro de masa del marco, se puede traducir la sección transversal diferencial - el ojo del toro cuando usted está…
Cómo trabajar con ecuaciones de dispersión de las partículas y de la sección transversal Los físicos cuánticos utilizan grandes aceleradores de partículas para descubrir más acerca de la dispersión de partículas a nivel subatómico. Usted puede pensar en un experimento de dispersión en términos de partículas en y partículas…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…