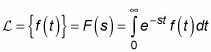Antes de que pueda resolver una ecuación diferencial, lo que necesita saber de qué tipo es. Hay varios tipos diferentes de ecuaciones, incluyendo lineal, separable, exacta y homogénea, y no homogénea.
Ecuaciones diferenciales lineales tratan exclusivamente con derivados a la primera potencia (se olvidan de derivados planteadas a cualquier poder superior).
El poder se hace referencia aquí es el poder del derivado se eleva a, no el orden de la derivada. Aquí hay una ecuación diferencial lineal bastante típico de aspecto:
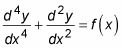
Ecuaciones diferenciales separables pueden ser escritos para que todos los términos en X y todos los términos de y aparecerá en lados opuestos de la ecuación, como se puede ver en este ejemplo:
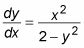
que también se puede escribir como
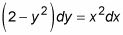
Ecuaciones diferenciales exactas son aquellos en los que se puede encontrar una función cuyo derivadas parciales corresponden a los términos de la ecuación diferencial. He aquí un ejemplo:
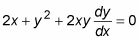
Ecuaciones diferenciales homogéneas sólo contienen derivados de y y las condiciones que implica y. Como se puede ver en esta ecuación, también están ajustados a 0:
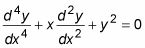
Ecuaciones diferenciales no homogéneas son las mismas que las ecuaciones diferenciales homogéneas, pero con una excepción: Sólo pueden tener términos implica X y / o constantes en el lado derecho. He aquí un ejemplo de una ecuación diferencial no homogénea:
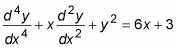
La solución general de esta ecuación diferencial no homogénea:
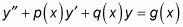
es
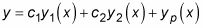
dónde c1y1 (X) + c2y2 (X) Es la solución general de la correspondiente ecuación diferencial homogénea
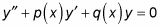
y yp(X) Es una solución particular de la ecuación no homogénea.
Dos maneras eficaces para resolver ecuaciones diferenciales
Puede resolver una ecuación diferencial en un número de maneras. Las dos técnicas más eficaces que puede utilizar son el método de coeficientes indeterminados y el método de series de potencias.
El método de coeficientes indeterminados es una forma útil para resolver ecuaciones diferenciales. Para aplicar este método, sólo tiene que conectar una solución que utiliza coeficientes constantes desconocidas en la ecuación diferencial y luego resolver esos coeficientes mediante el uso de las condiciones iniciales especificadas.
Series de potencia son una herramienta más en su ecuación diferencial toolkit resolver. Puede sustituir una serie de potencias como la siguiente en una ecuación diferencial:
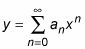
Entonces todo lo que tienes que hacer es encontrar una relación de recurrencia que le da el coeficiente lan.
Resolución de ecuaciones diferenciales con transformada de Laplace Soluciones
Transformadas de Laplace son un tipo de transformada integral que son ideales para hacer ecuaciones diferenciales revoltosos más manejable. Simplemente tomar la transformada de Laplace de la ecuación diferencial en cuestión, resolver esa ecuación algebraica, y tratar de encontrar la transformada inversa. Aquí está la transformada de Laplace de la función F (t):
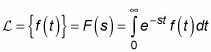
Echa un vistazo a esta tabla útil de transformadas de Laplace de funciones comunes cada vez que no desea tomar el tiempo para calcular una transformada de Laplace por su cuenta.