Analizar un circuito de primer orden rc usando métodos LaPlace

El uso de la transformada de Laplace como parte de su análisis de circuitos le proporciona una predicción de respuesta del circuito. Analizar los polos de la transformada de Laplace para obtener una idea general del comportamiento de salida. Polos reales, por ejemplo, indican el comportamiento de salida exponencial.

Siga estos pasos básicos para analizar un circuito utilizando técnicas de Laplace:

1. Desarrollar la ecuación diferencial en el dominio del tiempo usando las leyes de Kirchhoff y las ecuaciones de los elementos.

2. Aplicar la transformación de Laplace de la ecuación diferencial para poner la ecuación en la s-dominio.

3. Algebraicamente resolver para la solución, o la respuesta transformar.

4. Aplicar la transformación inversa de Laplace para producir la solución de la ecuación diferencial original descrito en el dominio del tiempo.

Para sentirse cómodo con este proceso, sólo hay que practicar su aplicación a diferentes tipos de circuitos tales como un RC (resistencia-condensador) de circuito, un RL (resistor-inductor) del circuito, y un (resistor-inductor-condensador) circuito RLC .

Considere el primer orden de circuito serie RC simple que se muestra aquí. Para configurar la ecuación diferencial para este circuito en serie, puede utilizar la ley de voltaje de Kirchhoff (LTK), que dice que la suma de las subidas de tensión y cae alrededor de un bucle es cero. Este circuito tiene la siguiente ecuación KVL alrededor del bucle:

-v_S(t) + v_r(t) + v_c(t) = 0

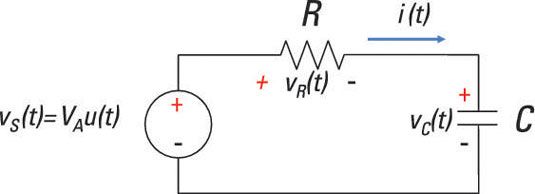
A continuación, la formulación de la ecuación elemento (o i-v característica) para cada dispositivo. La ecuación elemento para la fuente es

v_S(t) = V_LAu (t)

Utilice la ley de Ohm para describir la tensión en la resistencia:

v_R(t) = i (t) R

Elemento de la ecuación de El condensador se da como

Sustituyendo esta expresión para ello) dentro v_R(t) le da la siguiente expresión:

Sustituyendo v_R(televisión_C(t), y v_S(t) en la ecuación conduce a KVL

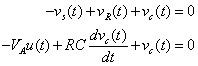
Ahora reorganizar la ecuación para obtener la ecuación diferencial de primer orden deseado:

Ahora está listo para aplicar la transformación de Laplace de la ecuación diferencial en el s-dominio. El resultado es

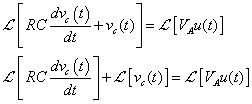
A la izquierda, la propiedad de linealidad se usó para tomar la transformada de Laplace de cada término. Para el primer término en el lado izquierdo de la ecuación, se utiliza la propiedad de diferenciación, que le da

Utiliza esta ecuación V_C(s) = # 8466- [v_C(t)], y V₀ es la tensión inicial a través del condensador.

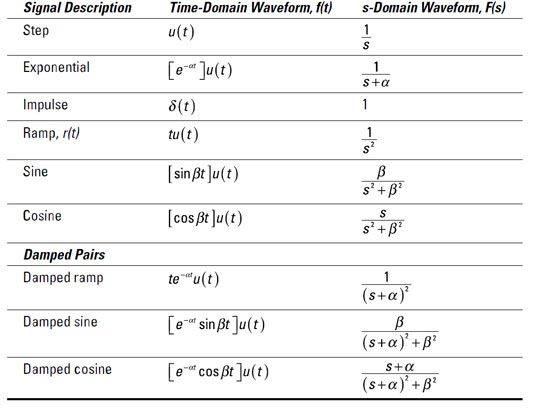
Utilizando la tabla siguiente, la transformada de Laplace de una función de paso le proporciona lo siguiente:

Sobre la base de las expresiones anteriores para las transformadas de Laplace, la ecuación diferencial se convierte en la siguiente:

A continuación, reorganizar la ecuación:

Resuelva para la salida V_c(s) obtener la siguiente transformar solución:

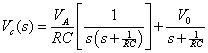
Mediante la realización de una transformada inversa de Laplace de V_C(s) para una condición inicial dada, esta ecuación conduce a la solución v_C(t) de la ecuación original diferencial de primer orden.

En el paso 3 del proceso. Para obtener la solución dominio del tiempo v_C(t), que tiene que hacer una expansión en fracciones parciales para el primer término del lado derecho de la ecuación anterior:

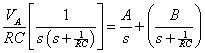
Es necesario determinar las constantes LA y B. Para simplificar la ecuación anterior, se multiplican ambos lados por s (s + 1 / RC) para deshacerse de los denominadores:

Algebraicamente reorganizar la ecuación mediante la recopilación de términos semejantes:

Para que el lado izquierdo de la ecuación anterior es cero, los coeficientes deben ser cero (A + B = 0 y A - V_LA = 0). Para constantes LA y B, terminas con A = V_LA y B = -V_LA. Sustituir estos valores en la ecuación siguiente:

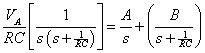
La sustitución que lleva a:

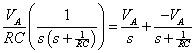
Ahora sustituir la expresión anterior en el V_C(s) ecuación para obtener la solución de transformar:

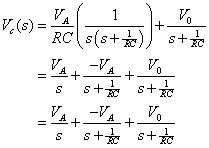
Esto completa la expansión en fracciones parciales. A continuación, puede utilizar la tabla dada anteriormente para encontrar la transformada inversa de Laplace para cada término del lado derecho de la ecuación anterior.

El primer término tiene la forma de una función escalonada, y los dos últimos términos tienen la forma de una exponencial, por lo que la transformada inversa de Laplace de la ecuación anterior que lleva a la siguiente solución v_C(t) en el dominio del tiempo:

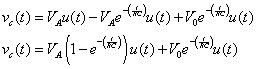
El resultado muestra el paso del tiempo t tiende a infinito, el condensador se carga con el valor de la entrada V_LA. Además, el voltaje inicial del condensador finalmente muere a cabo a cero después de un largo período de tiempo (aproximadamente 5 constantes de tiempo, RC).