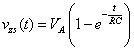Encuentra las respuestas de entrada cero y por el estado cero de un circuito RC serie

Para encontrar la respuesta total de un circuito RC en serie, es necesario encontrar la respuesta a entrada cero y la respuesta de estado cero y luego sumarlos. Un circuito en serie RC de primer orden tiene una resistencia (o de la red de resistencias) y un condensador conectado en serie.

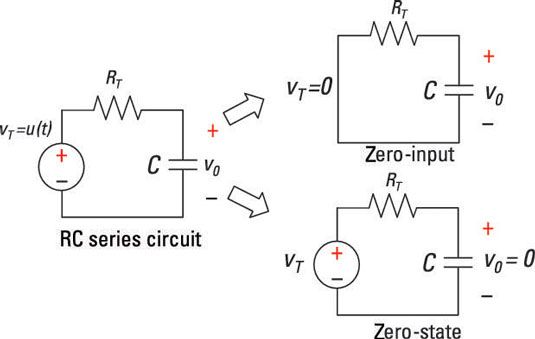
Este es un circuito serie RC divide en dos circuitos. El diagrama superior derecha muestra la respuesta de entrada cero, que se obtiene mediante el establecimiento de la entrada a 0. El diagrama inferior derecha muestra la respuesta de estado cero, que se obtiene mediante el establecimiento de las condiciones iniciales a 0.

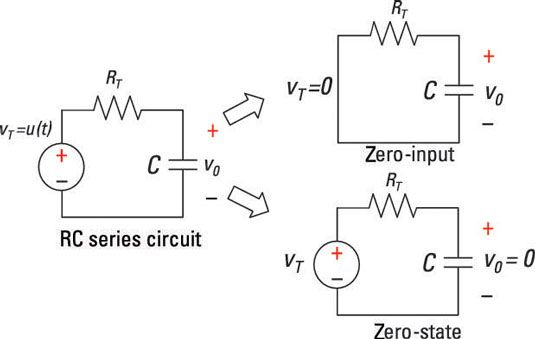
En primer lugar, quiere encontrar la respuesta a entrada cero para el circuito serie RC. El diagrama de arriba a la derecha aquí muestra la señal de entrada v_T(t) igual a 0. tensión cero de entrada significa que tiene cero. . . nada. . . zip. . . de entrada para todos los tiempos. La respuesta de salida se debe a la condición inicial V₀ (tensión del condensador inicial) en el tiempo t = 0. La ecuación diferencial de primer orden se reduce a

Aquí, v_ZI(t) es la tensión del condensador. Para una fuente de entrada se establece en 0 voltios como se muestra aquí, la tensión del condensador se llama respuesta de entrada cero o respuesta libre. No hay fuerzas externas (tales como una batería) están actuando en el circuito, excepto para el estado inicial de la tensión del condensador.

Usted puede adivinar razonablemente que la solución es la función exponencial (se puede comprobar y verificar la solución después). Intenta una exponencial debido a la derivada temporal de una exponencial también es una exponencial. Sustituto que adivina en la ecuación del circuito RC de primer orden:

v_ZI(t) = Ae^kt

los LA y k son constantes arbitrarias de la respuesta de entrada cero. Ahora sustituir la solución v_ZI(t) = Ae^kt en la ecuación diferencial:

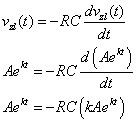
Usted obtiene una ecuación algebraica característica después de establecer la ecuación igual a 0 y factorizar Ae^kt:

Ae^kt(1 + la RCk) = 0

La ecuación característica le da un problema mucho más simple. El coeficiente de e^kt tiene que ser 0, por lo que sólo resolver para la constante k:

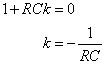
Cuando tengas k, usted tiene la respuesta de entrada cero v_ZI(t). Usando k = -1 / RC, usted puede encontrar la solución a la ecuación diferencial para la entrada de cero:

Ahora usted puede encontrar la constante LA mediante la aplicación de la condición inicial. En el momento t = 0, la tensión inicial es V₀, que le da

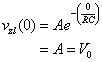
La constante LA es simplemente el voltaje inicial V₀ a través del condensador.

Por último, usted tiene la solución a la tensión del condensador, que es la respuesta de entrada cero v_ZI(t):

El término constante RC en esta ecuación se denomina constante de tiempo. La constante de tiempo proporciona una medida de cuánto tiempo un condensador se ha descargado o cargado. En este ejemplo, el condensador comienza en algún estado inicial de voltaje V₀ y disipa silenciosamente en el olvido a otro estado de 0 voltios.

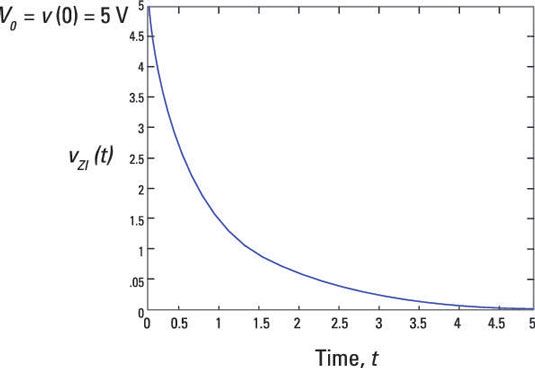
Suponer RC = 1 segundo y tensión inicial V₀ = 5 voltios. Este circuito de muestreo traza la exponencial en descomposición, mostrando que se tarda unos 5 constantes de tiempo, o 5 segundos, para la tensión del condensador a la descomposición a 0.

Encontrar la respuesta de estado cero, centrándose en la fuente de entrada

Respuesta Zero-estado significa condiciones iniciales nulas, y requiere de la búsqueda de la tensión del condensador cuando hay una fuente de entrada, v_T(t). Usted necesita encontrar las soluciones homogéneas y particulares para obtener la respuesta de estado cero. Para encontrar condiciones iniciales nulas, nos fijamos en el circuito cuando no hay tensión en el condensador en el tiempo t = 0.

El circuito en la parte inferior derecha de este circuito muestra tiene condiciones iniciales nulas y una tensión de entrada de V_T(t) = u (t), dónde u (t) es una entrada escalón unitario.

Matemáticamente, se puede describir la función de paso u (t) como

La señal de entrada se divide en dos intervalos de tiempo. Cuando t lt; 0, u (t) = 0. La ecuación diferencial de primer orden se convierte en

Usted ya ha encontrado la solución antes de tiempo t = 0, porque v_h(t) es la solución a la ecuación homogénea:

Usted determina la constante arbitraria c₁ después de encontrar la solución particular y la aplicación de la condición inicial V₀ de 0 voltios.

Ahora busca la solución particular vp (t) cuando u (t) = 1 después de t = 0.

Tiempo después t = 0, una entrada escalón unitario se describe el comportamiento de tensión transitoria a través del condensador. La tensión del condensador reaccionar a una entrada de paso se llama respuesta al escalón.

Para una entrada escalón v_T(t) = u (t), usted tiene una ecuación diferencial de primer orden:

Usted ya sabe que el valor de la etapa u (t) es igual a 1 después de t = 0. Sustituto u (t) = 1 en la ecuación anterior:

Resuelva para la tensión del condensador v_p(t), que es la solución particular. La solución particular siempre depende de la señal de entrada real.

Debido a que la entrada es una constante después de t = 0, la solución particular v_p(t) se supone que es una constante V_LA así como.

La derivada de una constante es 0, lo que implica lo siguiente:

Ahora sustituir v_p(t) = V_LA y su derivado en la ecuación diferencial de primer orden:

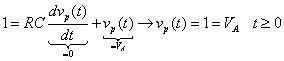
Después de un período relativamente largo de tiempo, la solución particular sigue a la entrada escalón unitario con la fuerza V_LA = 1. En general, una entrada escalón con la fuerza V_LA o V_LAu (t) conduce a una tensión del condensador de V_LA.

Después de encontrar las soluciones homogéneas y particulares, se suman las dos soluciones para obtener la respuesta de estado cero v_ZS(t). Tu encuentras c₁ mediante la aplicación de la condición inicial que es igual a 0.

Sumando la solución homogénea y la solución particular, usted tiene v_ZS(t):

v_ZS(t) = v_h(t) + v_p(t)

Sustituyendo en las soluciones homogéneas y particulares le da

A t = 0, la condición inicial es v_c(0) = 0 para la respuesta de estado cero. Ahora calcule v_ZS(0) como

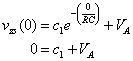
A continuación, resolver c₁:

c₁ = -V_LA

Sustituto c₁ en la ecuación de estado cero para producir la solución completa de la respuesta de estado cero v_ZS(t):