Analizar un segundo orden circuito paralelo RLC utilizando la dualidad

Circuitos RLC de segundo orden tienen una resistencia, inductor, y el condensador conectado en serie o en paralelo. Para analizar un circuito paralelo de segundo orden, se sigue el mismo proceso para el análisis de un circuito serie RLC.

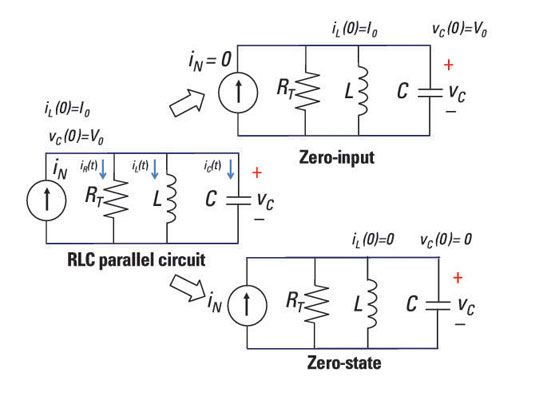
Aquí hay un ejemplo de RLC circuito paralelo. El diagrama de la izquierda muestra una entrada yo_N con corriente inicial inductor yo₀ y tensión del condensador V₀. El diagrama superior derecha muestra la fuente de corriente de entrada yo_N establece igual a cero, lo que permite resolver para la respuesta de entrada cero. El diagrama inferior derecha muestra las condiciones iniciales (yo₀ y V₀) Establece igual a cero, lo que le permite obtener la respuesta de estado cero.

Con la dualidad, que sustituye cada término eléctrica en una ecuación con su doble, o contraparte, y obtener otra ecuación correcta. Por ejemplo, el voltaje y la corriente son variables duales.

Establecer un circuito paralelo RLC típica

Debido a que los componentes del circuito paralelo de ejemplo mostrado anteriormente están conectados en paralelo, se configura la ecuación diferencial de segundo orden mediante el uso de la ley de Kirchhoff (KCL). KCL dice que la suma de las corrientes entrantes es igual a la suma de las corrientes salientes en un nodo. El uso de KCL en el nodo A del circuito de muestreo le da

yo_N(t) = i_R(t) + i_C(t) + i_L(t)

A continuación, poner la corriente de resistencia y la corriente del condensador en función de la corriente del inductor. La corriente resistor yo_R(t) se basa en la antigua ley, fiable de Ohm:

La restricción elemento para un inductor se da como

El actual yo_L(t) es la corriente del inductor, y L es la inductancia. Esta restricción significa una corriente variable genera una tensión de inductor. Si la corriente del inductor no cambia, no hay tensión inductor, lo que implica un cortocircuito.

Dispositivos paralelos tienen el mismo voltaje v (t). Se utiliza la tensión de inductor v (t) eso es igual a la tensión del condensador para obtener la corriente del condensador yo_C(t):

Ahora sustituir v (t) = LDI_L(t) / dt en la ley de Ohm, porque usted también tiene la misma tensión en la resistencia y el inductor:

Sustituye los valores de yo_R(t) y yo_C(t) en la ecuación KCL para darle las corrientes de dispositivos en función de la corriente del inductor:

El circuito paralelo RLC se describe mediante una ecuación diferencial de segundo orden, por lo que el circuito es un circuito de segundo orden. Lo desconocido es la corriente del inductor yo_L(t).

El análisis del circuito paralelo RLC sigue a lo largo de las mismas líneas que el circuito serie RLC. Comparar la ecuación anterior con esta ecuación de segundo orden derivado de la serie RLC:

Las dos ecuaciones diferenciales tienen la misma forma. La solución desconocida para el circuito RLC en paralelo es la corriente del inductor, y lo desconocido para el circuito RLC serie es la tensión del condensador. Estas incógnitas son variables duales.

Con dualidad, puede reemplazar cada término eléctrica en una ecuación con su doble y obtener otra ecuación correcta. Si utiliza la siguiente sustitución de variables en la ecuación diferencial para el circuito en serie RLC, se obtiene la ecuación diferencial para el circuito paralelo RLC.

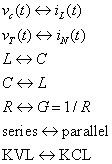
La dualidad le permite simplificar el análisis cuando se sabe resultados anteriores. Yippee!

Encuentra la respuesta de entrada cero

Los resultados que obtenga para un circuito paralelo RLC son similares a los que te dan para el circuito serie RLC. Para un circuito paralelo, tienes un segundo orden y la ecuación diferencial homogénea dada en términos de la corriente del inductor:

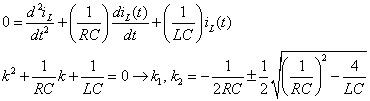
La ecuación anterior le da tres casos posibles bajo el radical:

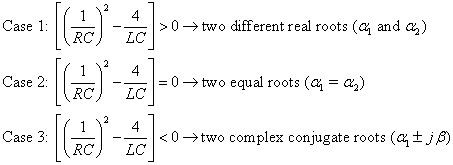
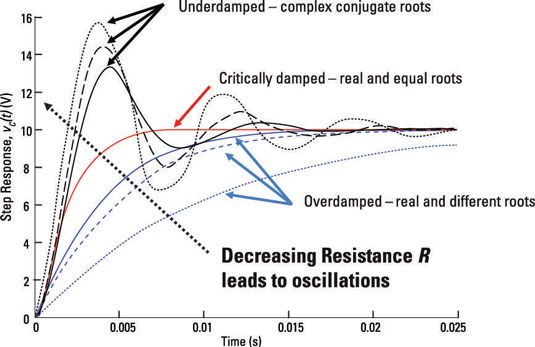
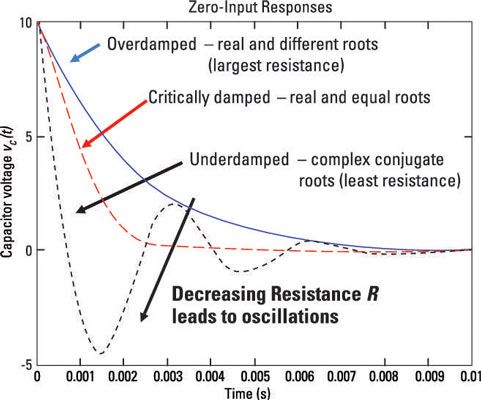
Las respuestas de entrada cero de las respuestas se asemejan a la forma del inductor se muestra aquí, que describe la tensión del condensador.

Cuando tengas k₁ y k₂, usted tiene la respuesta de entrada cero yo_ZI(t). La solución que da

Usted puede encontrar las constantes c₁ y c₂ mediante el uso de los resultados encontrados en el circuito en serie RLC, que se dan como

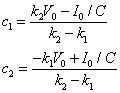
Aplicar la dualidad a la ecuación anterior reemplazando el voltaje, corriente, y la inductancia con sus duales (corriente, voltaje y capacitancia) para obtener c₁ y c₂ para el circuito paralelo RLC:

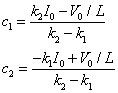
Después de conectar las variables duales, la búsqueda de las constantes c₁ y c₂ es fácil.

Llegue a la respuesta de estado cero

Respuesta Zero-estado significa condiciones iniciales nulas. Usted necesita encontrar las soluciones homogéneas y particulares de la corriente del inductor cuando hay una fuente de entrada yo_N(t). Cero condiciones iniciales significa mirar en el circuito cuando hay 0 corriente del inductor y 0 tensión del condensador.

Cuando t lt; 0, u (t) = 0. La ecuación diferencial de segundo orden se convierte en la siguiente, donde yo_L(t) es la corriente del inductor:

Para una entrada escalón donde u (t) = 0 antes de tiempo t = 0, la solución homogénea ih (t) es

Adición de la solución homogénea a la solución particular para una entrada escalón IAU (t) le da la respuesta en estado cero yo_ZS(t):

Ahora conecte los valores de yo_h(t) y yo_p(t):

Aquí están los resultados de C₁ y C₂ para el circuito serie RLC:

Ahora aplicar la dualidad a través de una simple sustitución de términos con el fin de obtener C₁ y C₂ para el circuito paralelo RLC:

Encuentra la respuesta total

Finalmente añadir la respuesta de entrada cero yo_ZI(t) y la respuesta de estado cero yo_ZS(t) para obtener la respuesta total yo_L(t):

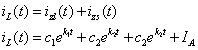
La solución se asemeja a los resultados para el circuito en serie RLC. Además, las respuestas a un escalón de la corriente del inductor siguen la misma forma que los mostrados en las respuestas a un escalón se encuentran en este circuito de muestreo, para la tensión del condensador.