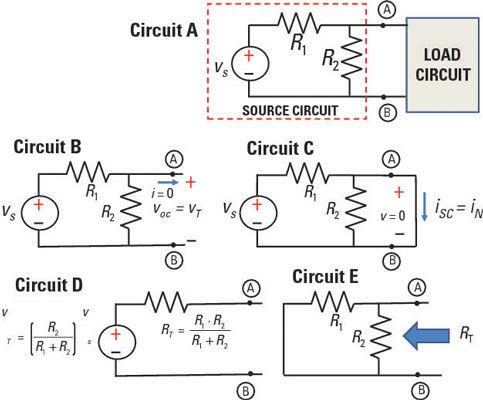
Encuentra ª & # 233-venin de y equivalentes de Norton para el circuito de la fuente compleja

Un Th # 233-venin o Norton circuito equivalente es valiosa para el análisis de las piezas de origen y de carga de un circuito. Th # del teorema de Norton 233-venin y le permiten reemplazar un complicado conjunto de fuentes y resistencias independientes, convirtiendo el circuito de la fuente en una sola fuente independiente conectada con una sola resistencia.

Utilizando el Th # 233-venin o Norton equivalente de un circuito le permite evitar tener que volver a analizar todo el circuito y otra vez, sólo para probar diferentes cargas.

Aplicar el teorema de Th # 233-venin al análisis de circuitos

Para simplificar el análisis, cuando la interconexión entre los circuitos de origen y de carga, el Th # método 233-venin sustituye a un circuito de fuente de complejo con una sola fuente de tensión en serie con una sola resistencia. Para obtener el Th # 233-venin equivalente, es necesario calcular el voltaje de circuito abierto v_oc y la corriente de cortocircuito yo_sc.

Un circuito que se muestra aquí es un circuito de fuente con una fuente de tensión independiente conectado a un circuito de carga. Circuito B muestra el mismo circuito, excepto que el circuito de carga se ha sustituido con una carga de circuito abierto. Utiliza la carga de circuito abierto para obtener el Th # tensión de 233-venin, v_T, a través de las terminales A y B. La tensión # 233-venin Th es igual a la tensión en circuito abierto, v_oc.

El voltaje es impulsado por una fuente de tensión para este circuito en serie, a fin de utilizar la técnica de divisor de tensión para obtener v_oc:

La solución para v_oc le da la Th # tensión de 233-venin, v_T.

Circuito C muestra el mismo circuito de fuente como una carga de cortocircuito. Utiliza la carga de cortocircuito para obtener la corriente de Norton, yo_N, a través de las terminales A y B. Y usted encontrar la corriente Norton encontrando la corriente de cortocircuito, yo_sc.

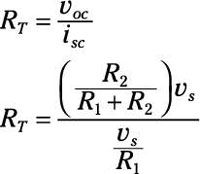
En Circuito C, el corto circuito está en paralelo con la resistencia R₂. Esto significa que toda la corriente que sale de resistor R₁ fluirá a través de la corta porque el corto tiene resistencia cero. En otras palabras, los by-pass cortos R₂. Usted puede encontrar la corriente a través de las terminales A y B utilizando la ley de Ohm, la producción de la corriente de cortocircuito:

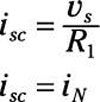
Esta corriente de cortocircuito, yo_sc, le da la corriente de Norton, yo_N.

Por último, para obtener el Th # resistencia 233-venin, R_T, se divide la tensión en circuito abierto por la corriente de cortocircuito. A continuación, terminará con la siguiente expresión para R_T:

Simplifique la ecuación para obtener el Th # resistencia 233-venin:

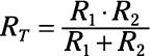
Circuito D muestra el Th equivalente # 233-venin para el circuito de la fuente en el circuito A.

La ecuación anterior se parece a la resistencia total para la conexión en paralelo entre las resistencias R₁ y R₂ cuando se corta (o eliminar) la fuente de tensión y mirar hacia atrás de las terminales A y B.

Al mirar a la izquierda de las terminales A y B, se puede encontrar el Th # resistencia 233-venin R_T mediante la eliminación de todas las fuentes independientes por un cortocircuito en las fuentes de tensión y la sustitución de fuentes de corriente con circuitos abiertos. Después de la eliminación de las fuentes independientes, se puede encontrar la resistencia total entre las terminales A y B, que se muestra en el Circuito E del circuito de muestreo. (Tenga en cuenta que esta táctica sólo funciona cuando no hay fuentes dependientes.)

Aplicar el teorema de Norton para el análisis de circuitos

Para ver cómo utilizar el enfoque de Norton para circuitos con múltiples fuentes, considere Circuito A en el circuito de muestreo se muestra aquí.

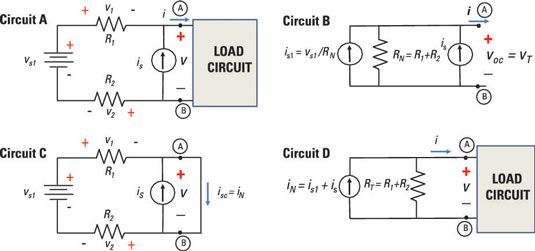
Debido a que no importa si usted encuentra la corriente de cortocircuito o el voltaje de circuito abierto en primer lugar, usted puede comenzar por la determinación de la tensión en circuito abierto. Poner una carga abierta en las terminales A y B resultados en circuito B. El siguiente análisis muestra cómo obtener yo_s1 y R_N en el circuito B.

La aplicación de la ley de voltaje de Kirchhoff (LTK) en Circuito A le permite determinar el voltaje de circuito abierto, v_oc. KVL dice que la suma de la tensión se eleva y cae alrededor del bucle es cero. Suponiendo una carga de circuito abierto para Circuito A, se obtiene la siguiente ecuación KVL (donde la carga es un circuito abierto, v = v_oc):

Algebraicamente resolver v_oc para obtener la tensión de circuito abierto:

La corriente suministrada por la fuente de voltaje v_s pasa a través de resistencias R₁ y R₂ debido a que la corriente que pasa a través de una carga de circuito abierto es igual a cero. En Circuito B, puede ver la fuente de corriente es como un dispositivo que tiene una resistencia infinita (es decir, como un circuito abierto).

Sin embargo, toda la corriente suministrada por la fuente de corriente es atravesará R₁ y R₂, y ninguno de la corriente desde yo_s pasará a través de la carga de circuito abierto. Aplicando la ley de Ohm (v = iR), Dispone de las siguientes tensiones a través de resistencias R₁ y R₂:

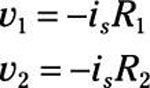
El signo menos aparece en estas ecuaciones porque la corriente de flujos es de sentido opuesto a las polaridades de voltaje asignados a través de las resistencias.

Sustituto v₁ y v₂ en la expresión de v_oc, y que terminan con la siguiente tensión en circuito abierto:

La tensión en circuito abierto es igual a la Th # 233-venin tensión equivalente, v_oc = v_T.

A continuación, encontrar la corriente de cortocircuito en el circuito C del circuito de muestreo se muestra aquí.

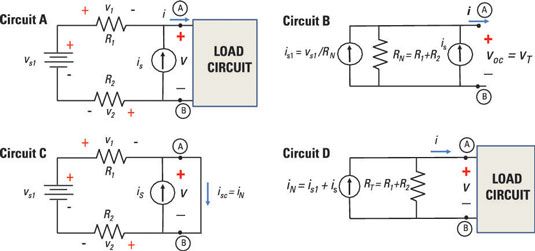
El actual yo_s1 suministrada por la fuente de tensión fluirá solamente a través de resistencias R₁ y R₂, no a través de la fuente de corriente yo_s, que tiene resistencia infinita. Debido al corto circuito, las resistencias R₁ y R₂ están conectados en serie, lo que resulta en una resistencia equivalente de R₁ + R₂. Aplicando la ley de Ohm a esta combinación en serie le da la siguiente expresión para yo_s1 proporcionada por la fuente de voltaje v_s1:

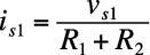
Ley de corriente de Kirchhoff (KCL) dice que la suma de las corrientes entrantes es igual a la suma de las corrientes salientes en un nodo. La aplicación de KCL en el nodo A, se obtiene

Sustituyendo la expresión para yo_s1 en la ecuación KCL anterior le da la corriente de cortocircuito, yo_sc:

La corriente de Norton yo_N es igual a la corriente de cortocircuito: yo_N = yo_sc.

Por último, se divide el voltaje de circuito abierto por la corriente de cortocircuito para obtener la resistencia Norton, R_N:

La conexión de las expresiones para v_oc y yo_sc le da la resistencia Norton:

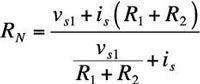
Adición de los términos en el denominador requiere la suma de fracciones, por lo que volver a escribir los términos por lo que tienen un denominador común. Algebraicamente, la ecuación se simplifica de la siguiente manera:

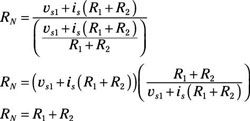
Cuando usted mira a la izquierda de la derecha de las terminales A y B, la resistencia Norton es igual a la resistencia total, mientras que la eliminación de todas las fuentes independientes. Usted ve el Norton equivalente en Circuito D del circuito de muestreo, donde R_T = R_N.