Analizar un circuito RC serie usando una ecuación diferencial

Un circuito en serie RC de primer orden tiene una resistencia (o de la red de resistencias) y un condensador conectado en serie. De primer orden circuitos RC se pueden analizar utilizando ecuaciones diferenciales de primer orden. Mediante el análisis de un circuito de primer orden, se puede entender el momento y retrasos.

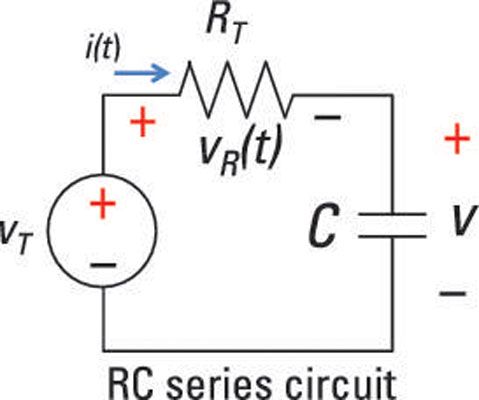
He aquí un ejemplo de una serie de primer orden circuito RC.

Si el circuito en serie RC tiene un condensador conectado con una red de resistencias en lugar de una sola resistencia, puede utilizar el mismo enfoque para analizar el circuito. Sólo tienes que encontrar el # 233-venin Th equivalente en primer lugar, la reducción de la red de resistencias a una sola resistencia en serie con una sola fuente de voltaje.

El circuito serie RC simple que se muestra aquí es impulsado por una fuente de tensión. Debido a que la resistencia y el condensador están conectados en serie, deben tener la misma corriente ello). Para el circuito de la muestra y lo que sigue a continuación, y mucho R = R_T.

Para encontrar el voltaje a través del resistor v_R(t), utiliza la ley de Ohm para un dispositivo de resistencia:

v_R(t) = Ri (t)

La restricción elemento para un condensador se da como

dónde v (t) es la tensión del condensador.

La generación de corriente a través de un condensador toma un voltaje cambiante. Si la tensión del condensador no cambia, la corriente en el condensador es igual a 0. Zero actual implica una resistencia infinita de voltaje constante a través del condensador.

Ahora sustituir la corriente del condensador i (t) = Cdv (t) / dt como ley de Ohm para la resistencia R, porque los mismos flujos de corriente a través de la resistencia y el condensador. Esto le da la tensión en la resistencia, v_R(t):

Ley de voltaje de Kirchhoff (KVL) dice que la suma de las subidas de tensión y deja caer alrededor de un bucle de un circuito es igual a 0. Usando KVL para la muestra de RC circuito en serie le da

v_T(t) = v_R(t) + v (t)

Ahora sustituir v_R(t) en KVL:

Ahora tiene una ecuación diferencial de primer orden, donde la función incógnita es la tensión del condensador. Conociendo la tensión en el condensador le da la energía eléctrica almacenada en un condensador.

En general, la tensión del condensador se refiere como una variable de estado debido a que la tensión del condensador describe el estado o comportamiento del circuito en cualquier momento.

Una manera fácil de recordar que las variables de estado - como la tensión del condensador v_C(t) y corriente del inductor yo_L(t) - describir la situación actual del circuito es pensar en la posición de su coche y velocidad instantánea como variables de estado de su coche. Si usted está corriendo por el camino majestuoso del Parque Nacional de las Montañas Rocosas, la posición GPS y la velocidad del coche describen el estado actual de su conducción.

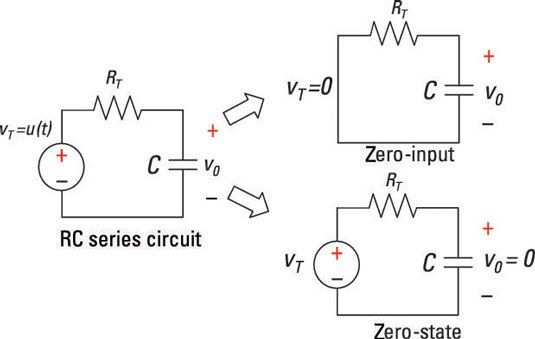
El circuito serie RC es un circuito de primer orden porque está descrito por una ecuación diferencial de primer orden. Un circuito reducido a tener un solo capacitancia equivalente y una sola resistencia equivalente es también un circuito de primer orden. El circuito tiene una tensión de entrada aplicada v_T(t).

Para encontrar la respuesta total de un circuito RC en serie, es necesario encontrar la respuesta a entrada cero y la respuesta de estado cero y luego sumarlos. Este es un circuito serie RC divide en dos circuitos. El diagrama superior derecha muestra la respuesta de entrada cero, que se obtiene mediante el establecimiento de la entrada a 0. El diagrama inferior derecha muestra la respuesta de estado cero, que se obtiene mediante el establecimiento de las condiciones iniciales a 0.