Analizar un circuito RL paralelo usando una ecuación diferencial

Un primer orden circuito en paralelo RL tiene una resistencia (o de la red de resistencias) y un único inductor. Circuitos de primer orden pueden ser analizadas usando las ecuaciones diferenciales de primer orden. Mediante el análisis de un circuito de primer orden, se puede entender el momento y retrasos.

Análisis de un circuito RL tales paralelos, como el que se muestra aquí, sigue el mismo proceso que el análisis de un circuito en serie RC. Así que si usted está familiarizado con este procedimiento, esto debe ser una brisa.

Si el circuito RL paralelo tiene un inductor conectado con una red de resistencias en lugar de una sola resistencia, puede utilizar el mismo enfoque para analizar el circuito. Pero usted tiene que encontrar el equivalente de Norton en primer lugar, la reducción de la red de resistencias a una sola resistencia en paralelo con una sola fuente de corriente.

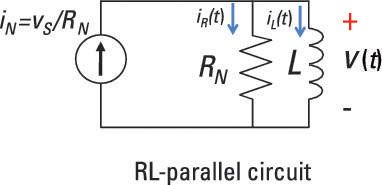
Comience con el circuito paralelo RL sencilla

Debido a que la resistencia y el inductor se conectan en paralelo en el ejemplo, deben tener el mismo voltaje v (t). La corriente resistor yo_R(t) se basa en la ley de Ohm:

La restricción elemento para un inductor se da como

dónde ello) es la corriente del inductor y L es la inductancia.

Usted necesita una corriente de voltaje para generar el cambio a través de un inductor. Si la corriente del inductor no cambia, no hay tensión inductor, lo que implica un cortocircuito.

Ahora sustituir v (t) = LDI (t) / dt como ley de Ohm porque tiene la misma tensión en la resistencia y el inductor:

Actual ley de Kirchhoff (KCL) dice que las corrientes entrantes son iguales a las corrientes salientes de un nodo. Utilice KCL en el nodo A del circuito de muestreo para obtener yo_N(t) = i_R(t) = i (t).

Sustituto yo_R(t) en la ecuación KCL para darle

El circuito RL paralelo es un circuito de primer orden porque está descrito por una ecuación diferencial de primer orden, donde la variable desconocida es la corriente del inductor ello). Un circuito que contiene un único inductor equivalente y una resistencia equivalente es un circuito de primer orden.

Conociendo la corriente del inductor le da la energía magnética almacenada en un inductor.

En general, la corriente del inductor se conoce como una variable de estado debido a que la corriente del inductor se describe el comportamiento del circuito.

Calcular la respuesta de entrada cero para un circuito RL paralelo

Así es como el circuito RL paralelo se divide en dos problemas: la respuesta de entrada cero y la respuesta de estado cero. Aquí, usted comenzará analizando la respuesta de entrada cero.

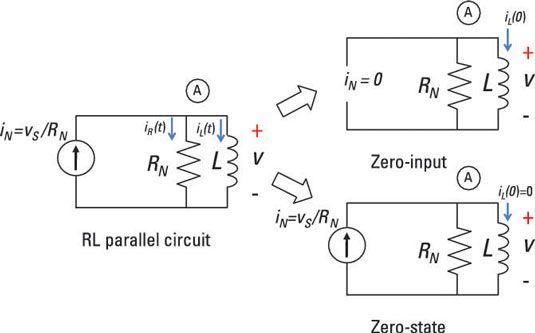
Para simplificar las cosas, se establece la fuente de entrada (o función forzada) igual a 0: yo_N(t) = 0 amperios. Esto significa que no hay corriente de entrada de todos los tiempos - un cero grande y gordo. La ecuación diferencial de primer orden se reduce a

Para una fuente de entrada de nadie, la corriente del inductor actual yo_Zyo se denomina una respuesta de entrada cero. No hay fuerzas externas están actuando en el circuito a excepción de su estado inicial (actual o inductor, en este caso). La salida es debido a alguna corriente inicial inductor yo₀ en el momento t = 0.

Usted hace una suposición razonable en la solución (la función exponencial natural!) Y sustituir su conjetura en la ecuación diferencial RL de primer orden. Asumir la corriente del inductor y la solución a ser

yo_ZI(t) = Be^kt

Esta es una suposición razonable porque la derivada temporal de una exponencial también es una exponencial. Como un buen amigo, la función exponencial no le fallará al resolver estas ecuaciones diferenciales.

Usted determina las constantes B y k Siguiente. Sustituya su conjetura yo_ZI(t) = Ser^kt en la ecuación diferencial:

Sustitución yo_ZI(t) con Ser^kt y haciendo un poco de matemática le da lo siguiente:

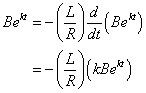
Usted tiene la ecuación característica después de factorizar Ser^kt:

La ecuación característica le da una problema algebraico para resolver la constante k:

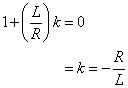
Usar k = -R / L y la corriente inicial inductor yo₀ a t = 0. Esto implica que B = I₀, por lo que la respuesta de entrada cero yo_ZI(t) le da la siguiente:

La constante L / R se llama la constante de tiempo. La constante de tiempo proporciona una medida de la duración de una corriente del inductor se necesita para ir a 0 o cambiar de un estado a otro.

Para analizar el circuito RL paralelo aún más, debe calcular respuesta de estado cero del circuito, y luego añadir el resultado a la respuesta de entrada cero a encontrar la respuesta total para el circuito.