Encuentra la respuesta total de un circuito paralelo rl
Después de encontrar la respuesta a entrada cero y la respuesta de estado cero de un circuito RL en paralelo, usted puede encontrar fácilmente la respuesta total del circuito. Recuerde que un circuito RL paralelo primer orden tiene una resistencia (o red de resistencias) y un único inductor.
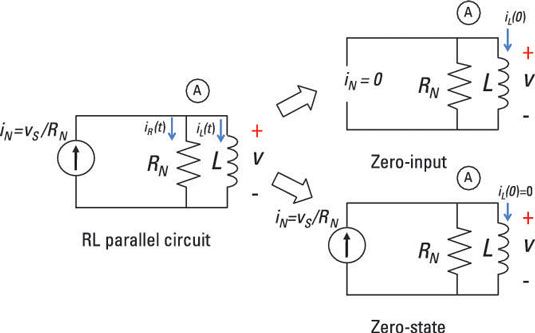
He aquí una muestra de circuito RL se muestra con respuesta de entrada cero y respuesta de estado cero. El diagrama superior derecha muestra la respuesta de entrada cero, que se obtiene mediante el establecimiento de la entrada a 0. El diagrama inferior derecha muestra la respuesta de estado cero, que se obtiene mediante el establecimiento de las condiciones iniciales a 0.
La ecuación diferencial de primer orden que usted necesita para encontrar la respuesta a entrada cero vZI(t) para este circuito.
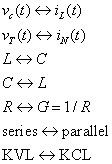
Después de aplicar sus habilidades matemáticas, a encontrar la respuesta a entrada cero del circuito:
Ahora para encontrar la respuesta en estado cero, es necesario estudiar el circuito bajo condiciones iniciales nulas mirando el circuito con corriente del inductor cero en t lt; 0. Usted necesita encontrar las soluciones homogéneas y particulares para obtener la respuesta de estado cero.
Después de aplicar sus habilidades matemáticas de nuevo, a encontrar la respuesta en estado cero del circuito:
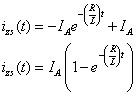
Para obtener la respuesta total para el circuito RL en paralelo, es necesario sumar las dos soluciones, las respuestas de entrada cero y por el estado de cero:
i (t) = iZJ(t) + iZS(t)
Sustituya las respuestas de entrada cero y por el estado cero de las secciones anteriores en esta ecuación, que le da
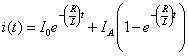
Echa un vistazo a la respuesta total para verificar la solución ello). Cuando t = 0, la corriente inicial es inductor
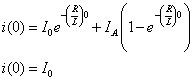
Esta es una afirmación verdadera - seguro, seguro. Si todavía no estás convencido, averiguar cuando la condición inicial se extingue. La salida solo se debe relacionar con la corriente de entrada o corriente paso para este ejemplo.
Después de un largo periodo de tiempo (5 constantes de tiempo), se obtiene lo siguiente:
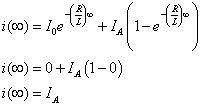
La corriente del inductor de salida es sólo la entrada escalonada teniendo una fuerza de yoLA. En otras palabras, la corriente del inductor alcanza un valor igual a la fuerza de la entrada escalón yoLA después de que la condición inicial desaparece en unos 5 constantes de tiempo de L / R, o 5L / R.
Usted ve las corrientes de inductor no cambian instantáneamente. Con inductores, las corrientes cambian gradualmente al pasar de un estado a otro. Una resistencia paralelo ralentiza las cosas. Es por eso que la constante de tiempo L / R tiene en cuenta cómo las corrientes de inductor rápido cambian de un estado a otro.
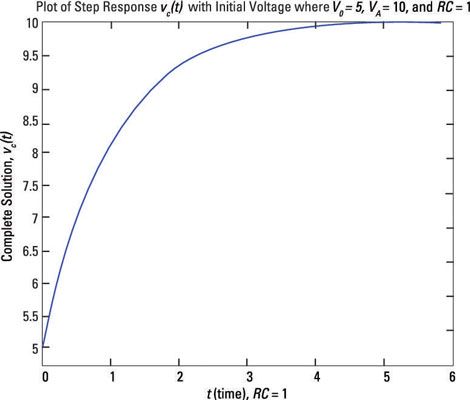
La respuesta completa de la corriente del inductor sigue la misma forma de la tensión del condensador se muestra aquí. La forma se inicia en algún corriente inicial y se va a otro estado actual después de 5 constantes de tiempo.
-
Analizar un circuito de primer orden rl utilizando métodos LaPlace -
Analizar un circuito de primer orden rc usando métodos LaPlace -
Analizar un circuito RC serie usando una ecuación diferencial -
Analizar un circuito RLC utilizando métodos LaPlace -
Crear paso banda y banda de rechazo filtros con circuitos en paralelo RLC -
Crear pasa banda y filtros con circuitos en serie RLC banda rechazar
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden Si usted puede utilizar una ecuación diferencial de segundo orden para describir el circuito que está viendo, entonces usted está tratando con un circuito de segundo orden. Circuitos que incluyen un inductor, condensador y resistencia conectada…
Describir inductores de circuito y calcular su almacenamiento de energía magnética En los circuitos, inductores resisten cambios instantáneos en energía magnética actual y tienda. Inductores son dispositivos electromagnéticos que encuentran un uso intensivo de radiofrecuencia circuitos (RF). Sirven de RF " estrangulaciones, "…
Componentes de la electrónica: la retroalimentación en los amplificadores de bucle cerrado Si usted está interesado en la comprensión de cómo funciona el circuito de realimentación, recuerde esta regla de amplificadores operacionales electrónicos: Si la tensión de entrada es otra cosa que no sea cero, el amplificador operacional se…
Componentes de la electrónica: cómo utilizar un amplificador operacional como un amplificador de ganancia unitaria LA amplificador de ganancia unitaria es un circuito amplificador electrónico que no amplifica. En otras palabras, tiene una ganancia de 1. La tensión de salida en un amplificador de ganancia unidad es la misma que la tensión de entrada.Usted…
Encuentra th & # 233-Venin y Norton circuitos equivalentes usando transformación fuente Un Th # 233-venin o Norton circuito equivalente es valiosa para el análisis de las piezas de origen y de carga de un circuito. Th # de los teoremas de Norton 233-venin y le permiten reemplazar un complicado conjunto de fuentes y resistencias…
Encuentra ª & # 233-venin de y equivalentes de Norton para el circuito de la fuente compleja Un Th # 233-venin o Norton circuito equivalente es valiosa para el análisis de las piezas de origen y de carga de un circuito. Th # del teorema de Norton 233-venin y le permiten reemplazar un complicado conjunto de fuentes y resistencias…
Encuentra la respuesta de estado cero de un circuito paralelo rl Un primer orden circuito en paralelo RL tiene una resistencia (o de la red de resistencias) y un único inductor. Circuitos de primer orden pueden ser analizadas usando las ecuaciones diferenciales de primer orden. Mediante el análisis de un…
Medidor de máxima transferencia de potencia utilizando ª & # 233-venin de y los teoremas de norton Th # teoremas de Norton de 233-venin y se pueden utilizar para analizar circuitos complejos, centrándose en los circuitos de fuente y carga. Una aplicación de Th # 233-venin de y los teoremas de Norton es calcular la potencia máxima para un…
Cómo detectar un impulso faltante con un circuito de temporización Cuando el tiempo es apagado en su ordenador, eventos específicos no se presentan en el orden correcto. Pero si usted sabe la física y yo-v relaciones de resistencias y condensadores, puede crear un circuito que pulses- detecta a continuación,…
Analizar un circuito RL paralelo usando una ecuación diferencial Un primer orden circuito en paralelo RL tiene una resistencia (o de la red de resistencias) y un único inductor. Circuitos de primer orden pueden ser analizadas usando las ecuaciones diferenciales de primer orden. Mediante el análisis de un…
Analizar un segundo orden circuito paralelo RLC utilizando la dualidad Circuitos RLC de segundo orden tienen una resistencia, inductor, y el condensador conectado en serie o en paralelo. Para analizar un circuito paralelo de segundo orden, se sigue el mismo proceso para el análisis de un circuito serie RLC.Aquí hay…
Encuentra la respuesta total de un circuito RC serie Después de encontrar la respuesta a entrada cero y la respuesta de estado cero de un circuito en serie RC, usted puede encontrar fácilmente la respuesta total del circuito. Recuerde que un circuito en serie RC de primer orden tiene una resistencia…