Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden

Si usted puede utilizar una ecuación diferencial de segundo orden para describir el circuito que está viendo, entonces usted está tratando con un circuito de segundo orden. Circuitos que incluyen un inductor, condensador y resistencia conectada en serie o en paralelo son circuitos de segundo orden. Aquí están los circuitos de segundo orden impulsado por una fuente de entrada, o de la función forzar.

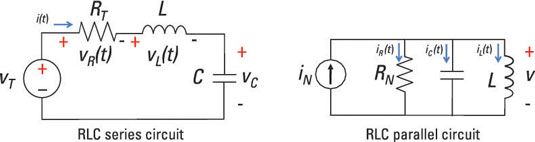
Conseguir una solución única a una ecuación diferencial de segundo orden requiere el conocimiento de los estados iniciales del circuito. Para un circuito de segundo orden, lo que necesita saber la tensión del condensador inicial y la corriente inicial inductor. Conociendo estos estados en la t = 0 le proporciona una solución única para todos los tiempos después de la hora t = 0.

Siga estos pasos en la resolución de una ecuación diferencial de segundo orden para un circuito de segundo orden:

1. Encuentra la respuesta de entrada cero mediante el establecimiento de la fuente de entrada a 0, tal que la salida se debe sólo a las condiciones iniciales.

2. Encuentra la respuesta de estado cero mediante el establecimiento de las condiciones iniciales igual a 0, tal que la salida se debe sólo a la señal de entrada.

   Cero condiciones iniciales significa que tiene 0 tensión del condensador inicial y 0 corriente inicial inductor.

   La respuesta de estado cero requiere que encontrar las soluciones homogéneas y particulares:

3. Solución homogénea: Cuando no hay señal de entrada o forzar la función - es decir, cuando v_T(t) = 0 o yo_N(t) = 0 - usted tiene la solución homogénea.

4. Solución particular: Cuando se tiene una entrada diferente de cero, la solución sigue la forma de la señal de entrada, que le da la solución particular. Por ejemplo, si su entrada es una constante, entonces su solución particular es también una constante. Del mismo modo, si usted tiene un seno o función coseno como entrada, la salida es una combinación de funciones seno y coseno.

5. Sume las respuestas de entrada cero y por el estado cero para obtener la respuesta total.

   Debido a que usted está tratando con circuitos lineales, desea utilizar la superposición para encontrar la respuesta total.

Para encontrar la respuesta total para una ecuación diferencial de segundo orden con coeficientes constantes, primero debe encontrar la solución homogénea utilizando una ecuación característica algebraica y asumir las soluciones son funciones exponenciales. Las raíces de la ecuación característica le dan las constantes que se encuentran en el exponente de la función exponencial.

Adivina en una solución primaria: La función exponencial natural,

Esta es sólo una aproximación a la solución de los circuitos de segundo orden. La buena noticia es que convierte un problema que involucra una ecuación diferencial a una que sólo utiliza el álgebra.

Considere la siguiente ecuación diferencial como un ejemplo numérico con cero función forzada v_T(t) = 0:

La solución a esta ecuación diferencial se llama la solución homogénea v (t). Un enfoque clásico implica dar su mejor oportunidad de adivinar la solución. Probar v (t) = e^kt. La función exponencial trabaja para una ecuación de primer orden, por lo que debe trabajar para una ecuación de segundo orden, también.

Cuando usted toma la derivada de la exponencial naturales e^kt, usted consigue lo mismo multiplicado por una constante k. Verá cómo la función exponencial es tu verdadero amigo en la solución de ecuaciones diferenciales como este.

A partir del cálculo de álgebra: El uso de la ecuación característica

Para resolver una ecuación diferencial homogénea, puede convertir la ecuación diferencial en una ecuación característica, que a resolver utilizando el álgebra. Esto se hace mediante la sustitución de su conjetura v (t) = e^kt desde temprano en la ecuación diferencial homogénea:

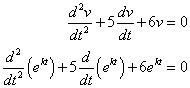
Factoring cabo e^kt que conduce a una ecuación característica:

(k² + 5k +6)e^kt = 0

El coeficiente de e^kt debe ser 0, para que puedas resolver k como sigue:

k² + 5k + 6 = 0k = -2. -3

Ajuste de la ecuación algebraica a 0 le da una ecuación característica. Las raíces constantes -2 y -3 determinan las características de la solución v (t).

A partir de estas raíces, se obtiene una solución homogénea que es una combinación de las soluciones e^-2t y e^-3t:

v (t) = c₁e^-2t + c₂e^-3t

Las constantes c₁ y c₂ están determinados por las condiciones iniciales cuando t = 0.