¿Cómo resolver ecuaciones diferenciales usando amplificadores operacionales

El circuito amplificador operacional puede resolver ecuaciones matemáticas rápidas, incluyendo problemas de cálculo, tales como las ecuaciones diferenciales. Para resolver una ecuación diferencial mediante la búsqueda v (t), por ejemplo, podría utilizar varias configuraciones del amplificador operacional para encontrar la tensión de salida v_o(t) = v (t).

Para simplificar el problema, asumir condiciones iniciales nulas: cero tensión del condensador inicial para cada integrador como se muestra aquí. Para resolver una ecuación diferencial, es necesario desarrollar un diagrama de bloques para la ecuación diferencial (que está representado por las cajas de trazos en la figura), dando a la entrada y la salida para cada cuadro de líneas discontinuas. A continuación, utilice el diagrama de bloques para diseñar un circuito.

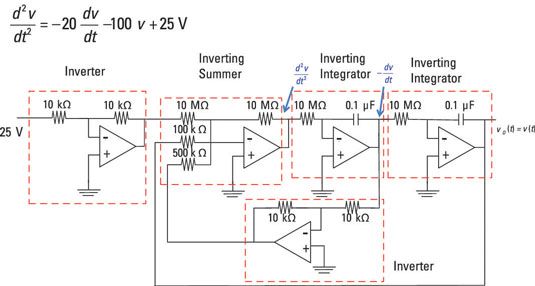
En el extremo izquierdo de la figura es una función de fuerza de 25 voltios derivados de los siguientes pasos: la tensión de salida v_o(t) = v (t) está en el extremo derecho.

Estos son los pasos básicos para diseñar el circuito:

1. Resolver para la derivada de orden más alto, mostrando que se compone de una suma de las derivadas inferiores.

   Suponga que quiere resolver la siguiente ecuación diferencial de segundo orden:

   

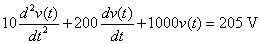
   El primer paso es resolver algebraicamente para la derivada de mayor orden, d²v / dt²:

   

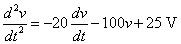
   La derivada de mayor orden es una combinación o suma de derivados más bajos y la tensión de entrada más pequeño: dv / dt, v, y 25. Por lo tanto, es necesario un verano de inversión para agregar los tres términos, y estos términos están obligando a las funciones (o entradas) para el verano inversora.

2. Utilice integradores para ayudar a implementar el diagrama de bloques, ya que la integral de la derivada de orden superior es el derivado que es un orden inferior.

   Para este ejemplo, integrar la segunda derivada, d²v / dt², para darle la primera derivada, dv / dt. Como se muestra aquí, la salida del amplificador inversor sumando es la segunda derivada (que es también la entrada a la primera integrador).

   La salida del primer integrador inversora es el negativo de la primera derivada dv / dt y sirve como la entrada al segundo integrador inversora. Con el segundo integrador inversora se muestra en la figura, integrar el negativo de la primera derivada, -dv / dt, para darle la salida deseada, v (t).

3. Tome las salidas de los integradores, escalarlos, y darles de comer de nuevo a un (amplificador sumador) de verano.

   La segunda derivada consiste en una suma de tres términos, por lo que este es el lugar donde el amplificador operacional inversor verano entra.

1. Una de las entradas es una constante de 25 voltios a el verano y habrá una tensión de entrada (o de conducción) fuente. Los 25 voltios a la entrada se alimenta a una de las entradas al verano con una ganancia de 1.

2. La salida del primer integrador es la primera derivada de v (t), que tiene un peso de 20 y se alimenta a la segunda entrada del sumador inversor.

3. La salida del segundo integrador se alimenta a la tercera entrada para el verano inversora con un peso de 100.

Esto completa el diagrama de bloques.

Para este ejemplo, se multiplica la primera derivada dv / dt por -10 y se multiplican v por -100. Suma como se muestra en el diagrama de bloques.

El circuito de ejemplo que se muestra aquí es uno de muchos diseños posibles. Pero se puede aplicar este proceso básico para resolver sus ecuaciones diferenciales utilizando amplificadores operacionales.