¿Cómo encontrar conmutadores de momento angular, l
En la física cuántica, usted puede encontrar conmutadores de momento angular, L. Primera examinar LX, Ly, y yoz por echar un vistazo a la forma en que commute- si conmutan (por ejemplo, si [LX, Ly] = 0), entonces se puede medir cualquier dos de ellos (LX y yoy, por ejemplo) exactamente. Si no es así, entonces están sujetos a la relación de incertidumbre, y no se puede medir de forma simultánea con exactitud.
Bien, así que ¿cuál es el colector de LX y yoy? El uso de LX = YPz - ZPy y yoy = ZPX - XPz, usted puede escribir lo siguiente:
[LX, Ly] = [YPz - ZPy, ZPX - XPz]
Puede escribir esta ecuación como
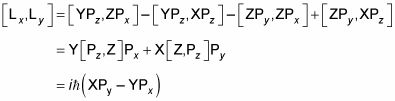
Pero
Así LX y yoy no conmutan, lo que significa que no se puede medir a ambos al mismo tiempo con total precisión. También puede demostrar que
Debido a que ninguno de los componentes del momento angular conmutar entre sí, no se puede medir cualquier dos a la vez con total precisión. Ratas.
Eso significa también que la LX, Ly, y yoz los operadores no pueden compartir los mismos estados propios. Entonces que puedes hacer? ¿Cómo puede usted encontrar un operador que comparte estados propios con los diversos componentes de L de modo que usted puede escribir los estados propios como | l, m>?
El truco habitual es que el cuadrado del momento angular, L2, es un escalar, no un vector, por lo que va a conmutar con la LX, Ly, y yoz operadores, no hay problema:
[L2, LX] = 0
[L2, Ly] = 0
[L2, Lz] = 0
Está bien, fresco, usted está haciendo progresos. Debido LX, Ly, y yoz no viajar, no se puede crear un estado propio que enumera los números cuánticos de dos de ellos. Pero debido a L2 conmuta con ellos, usted puede construir estados propios que tienen valores propios para L2 y uno cualquiera de LX, Ly, y yoz. Por convención, la dirección que se elige generalmente es Lz.
Cómo operadores de spin se asemejan a los operadores del momento angular Debido giro es un tipo de momento angular incorporado, operadores de spin tienen mucho en común con los operadores de momento angular orbital. A medida que su instructor de la física cuántica le dirá, hay operadores de spin análogas, S2 y Sz,…
Cómo organizar eingenvectors En la física cuántica, los vectores propios de un operador hermítica definen un conjunto completo de vectores ortonormales - es decir, una base completa para el espacio de estados. Cuando se ve en este " base propia, " que se construye de los…
Cómo calcular la degeneración de energía de un átomo de hidrógeno en términos de n, l, m y Cada estado cuántico del átomo de hidrógeno se especifica con tres números cuánticos: n (el número cuántico principal), l (el número cuántico del momento angular del electrón), y m (el z componente del momento angular del…
¿Cómo cambiar las coordenadas rectangulares a coordenadas esféricas En la física cuántica, para encontrar las funciones propias reales (no sólo los estados propios) de los operadores de momento angular como L2 y yoz, te apartas de coordenadas rectangulares, X, y, y z, a coordenadas esféricas, ya que va a hacer…
Cómo crear estados propios del momento angular Puede crear los estados propios reales, | l, m>, de estados de momento angular en la mecánica cuántica. Cuando usted tiene los estados propios, usted también tiene los valores propios, y cuando se tiene los valores propios, puede resolver el…
Cómo determinar estados propios osciladores armónicos de un sistema En la física cuántica, cuando tienes los estados propios de un sistema, se puede determinar los estados permitidos de sistema y la probabilidad relativa de que el sistema estará en cualquiera de esos estados.El conmutador de los operadores A, B…
¿Cómo encontrar valores propios del momento angular Cuando usted tiene los valores propios de estados de momento angular en la mecánica cuántica, puede resolver el hamiltoniano y obtener los niveles de energía permitidos de un objeto con el momento angular. Los valores propios del momento angular…
¿Cómo encontrar el conmutador de operadores En la física cuántica, la medida de lo diferente que es de aplicar el operador A y B, frente a B y luego A, se llama de los operadores conmutador. Así es como se define el colector de los operadores A y B:Dos operadores conmutar uno con el otro,…
¿Cómo encontrar los vectores propios y valores propios de un operador En la física cuántica, si te dan un operador en forma de matriz, usted puede encontrar sus vectores propios y valores propios. Por ejemplo, digamos que usted necesita para resolver la siguiente ecuación:En primer lugar, se puede reescribir esta…
Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación…
¿Cómo trabajar con vectores propios y eingenvalues En la física cuántica, al trabajar con mercados, es útil saber cómo utilizar vectores propios y valores propios. La aplicación de un operador a un ket puede dar lugar a una nueva ket:Para facilitar las cosas, se puede trabajar con vectores…
Matrices de Pauli En la física cuántica, cuando se trabaja con estados propios de spin y operadores para partículas de espín 1/2 en términos de matrices, es posible que vea los operadores SX, Sy, y Sz escrito en términos de Pauli matrices,Teniendo en cuenta que…