¿Cómo encontrar los vectores propios y valores propios de un operador
En la física cuántica, si te dan un operador en forma de matriz, usted puede encontrar sus vectores propios y valores propios. Por ejemplo, digamos que usted necesita para resolver la siguiente ecuación:
En primer lugar, se puede reescribir esta ecuación como la siguiente:
I representa la matriz identidad, con 1s a lo largo de su diagonal y 0s de otra manera:
Recuerde que la solución a
existe sólo si el determinante de la matriz A - laI es 0:
det (A - laI) = 0
¿Cómo encontrar los valores propios
Cualquier valor de la que satisfacen la ecuación det (A - laI) = 0 son valores propios de la ecuación original. Trate de encontrar los valores propios y vectores propios de la matriz siguiente:
En primer lugar, convertir la matriz en la forma A - laYO:
A continuación, encontrará el determinante:
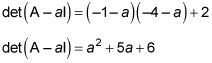
Y esto puede tenerse en cuenta como sigue:
Usted sabe que det (A - laI) = 0, por lo que los valores propios de A son las raíces de esta equation- saber, la1 = -2 Y la2 = -3.
¿Cómo encontrar los vectores propios
¿Cómo sobre la búsqueda de los vectores propios? Para encontrar el vector propio correspondiente a la1, sustituto la1 - el primer valor propio, -2 - en la matriz en la forma A - laYO:
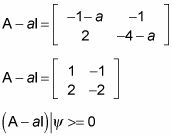
Así que tienes
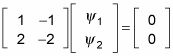
Debido a que cada fila de esta ecuación de la matriz debe ser verdad, usted sabe que
Y eso significa que, hasta una constante arbitraria, el vector propio correspondiente a la1 es la siguiente:
La caída de la constante arbitraria, y acaba de escribir esto como una matriz:
¿Qué te parece el vector propio correspondiente a la2? Tapar la2, -3, en la matriz en A -laYo formo, se obtiene lo siguiente:
Entonces tiene
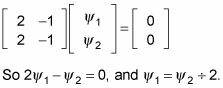
Y eso significa que, hasta una constante arbitraria, el vector propio correspondiente a la2 es
La caída de la constante arbitraria:
Así que los valores propios de este operador de matriz
son la1 = -2 Y la2 = -3. Y el vector propio correspondiente a la1 es
El vector propio correspondiente a la2 es
Cómo utilizar las operaciones normales en una matriz en la r Probablemente la característica más fuerte de R es su capacidad para hacer frente a operaciones con matrices complejas de una manera fácil y optimizado. Debido a que gran parte de las estadísticas se reduce a operaciones con matrices, es natural…
Comandos de la calculadora de álgebra lineal Las calculadoras gráficas son herramientas maravillosas para ayudar a resolver el álgebra lineal procesos- que le permiten descargar la batería más que el poder del cerebro. Dado que existe una amplia variedad de calculadoras gráficas por ahí,…
¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…
Cómo construir vectores en r LA vector es el tipo más simple de estructura de datos en el manual de R. El R define un vector como se " una sola entidad que consiste en una colección de cosas ". Una colección de números, por ejemplo, es un vector numérico - los primeros…
Cómo crear vectores en r Para crear un vector de una simple secuencia de números enteros, por ejemplo, se utiliza el operador coma (:) En R. El código de 3: 7 le da un vector con los números 3 a 7, y 4: -3 crea un vector con los números 4 a -3, tanto en pasos de 1.Para…
Cómo agregar vectores juntos Se le pide con frecuencia para añadir vectores en la resolución de problemas de física. Para sumar dos vectores, se colocan la cabeza a la cola y luego encontrar la duración y magnitud del resultado. El orden en que se agregan los dos vectores…
Cómo organizar eingenvectors En la física cuántica, los vectores propios de un operador hermítica definen un conjunto completo de vectores ortonormales - es decir, una base completa para el espacio de estados. Cuando se ve en este " base propia, " que se construye de los…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
¿Cómo encontrar componentes de un vector Puede convertir de la manera magnitud / ángulo de la especificación de un vector para la forma de coordenadas de expresión. Si lo hace, es esencial para los tipos de operaciones que puede esperar para ejecutar en vectores, tales como cuando se…
¿Cómo encontrar los valores propios y vectores propios para hamiltonianos degenerados El uso de la física cuántica, se puede determinar la F valores y vectores propios coincidencia para sistemas en los que las energías son degenerados. Echa un vistazo a este hamiltoniano no perturbado:En otras palabras, varios estados tienen la…
¿Cómo trabajar con vectores propios y eingenvalues En la física cuántica, al trabajar con mercados, es útil saber cómo utilizar vectores propios y valores propios. La aplicación de un operador a un ket puede dar lugar a una nueva ket:Para facilitar las cosas, se puede trabajar con vectores…
La física cuántica y el hamiltoniano Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…