Cómo determinar estados propios osciladores armónicos de un sistema
En la física cuántica, cuando tienes los estados propios de un sistema, se puede determinar los estados permitidos de sistema y la probabilidad relativa de que el sistema estará en cualquiera de esos estados.
El conmutador de los operadores A, B es [A, B] = AB - BA, por lo que el conmutador en cuenta de
es la siguiente:
Esto es igual a lo siguiente:
Esta ecuación se descompone en
Y la elaboración de esta ecuación con el hamiltoniano,
De acuerdo, con las relaciones del colector, ya está listo para ir. La primera pregunta es: si la energía del estado | n > Es En, ¿cuál es la energía del estado la | n >? Bueno, para encontrar esto, reorganizar el conmutador
A continuación, utilice esto para escribir la acción de
Me gusta esto:
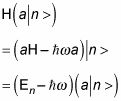
Así la | n > También es un estado propio del oscilador armónico, con la energía
Notan. Es por eso la se llama la aniquilación o bajar Operador: Reduce el nivel de energía de un estado propio oscilador armónico en un nivel.
¿Cuál es el nivel de energía de
Usted puede escribir que de esta manera:
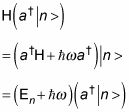
Todo esto significa que
es un estado propio del oscilador armónico, con la energía
no sólo En - eso es el
eleva el nivel de energía de un estado propio del oscilador armónico en un nivel.
Así que ya sabes que
Puede derivar lo siguiente de estas ecuaciones:
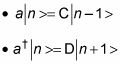
C y D son constantes positivas, pero ¿qué son iguales? Los estados |n - 1> y |n + 1> tienen que ser normalizado, lo que significa que lt;n - 1 |n - 1> = lt;n + 1 |n + 1> = 1. Así que echemos un vistazo a la cantidad usando el operador C:
Y porque |n - 1> es normalizado, lt;n - 1 |n - 1> = 1:
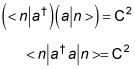
Pero usted también sabe que
el operador de nivel de energía, por lo que se obtiene la siguiente ecuación:
lt; n | N | n > = C2
N | n > = n | n >, Donde n es el nivel de energía, por lo que
n lt; n | n > = C2
Sin embargo, lt; n | n > = 1, por lo que
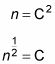
Este último le dice, desde la | n > = C | n - 1>, que
Eso está bien - ahora usted sabe cómo utilizar el operador de la reducción, la, en estados propios del oscilador armónico.
¿Qué pasa con el operador de fondos,
Primero reorganizar el conmutador
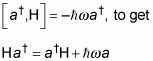
Luego sigue el mismo curso del razonamiento se toma con el la operador para mostrar lo siguiente:
Así que en este punto, ya sabes lo que los valores propios de la energía y cómo la subida y bajada operadores afectan los estados propios del oscilador armónico.
¿Cómo encontrar el nivel de energía de un oscilador armónico: un ejemplo Su instructor física cuántica puede pedirle que encontrar el nivel de energía de un oscilador armónico. La mejor manera de aprender es a través de un ejemplo. Digamos que usted tiene un protón someterse oscilación armónica concomo se muestra…
¿Cómo encontrar los valores propios y vectores propios para hamiltonianos degenerados El uso de la física cuántica, se puede determinar la F valores y vectores propios coincidencia para sistemas en los que las energías son degenerados. Echa un vistazo a este hamiltoniano no perturbado:En otras palabras, varios estados tienen la…
¿Cómo encontrar la energía de un oscilador cargada utilizando la teoría de la perturbación En la física cuántica, cuando se tiene los valores propios exactas para un oscilador cargada en un sistema perturbado, puede encontrar la energía del sistema. Basado en la teoría de la perturbación, la energía corregida del oscilador está…
¿Cómo encontrar el estado propio de energía de un oscilador armónico en el espacio posición En la física cuántica, puede utilizar los operadores para determinar el estado propio de energía de un oscilador armónico en el espacio posición. El encanto de la utilización de los operadores la yes que, dado el estado de la tierra, | 0>, los…
¿Cómo encontrar los vectores propios y valores propios de un operador En la física cuántica, si te dan un operador en forma de matriz, usted puede encontrar sus vectores propios y valores propios. Por ejemplo, digamos que usted necesita para resolver la siguiente ecuación:En primer lugar, se puede reescribir esta…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación…
Cómo utilizar los operadores para las cantidades de la física cuántica En la física cuántica, puede utilizar los operadores para ampliar las capacidades de sujetadores y mercados. A pesar de que han nombres que suena intimidante como Hamilton, la unidad, la pendiente, el momento lineal y Laplaciano, estos operadores…
¿Cómo trabajar con vectores propios y eingenvalues En la física cuántica, al trabajar con mercados, es útil saber cómo utilizar vectores propios y valores propios. La aplicación de un operador a un ket puede dar lugar a una nueva ket:Para facilitar las cosas, se puede trabajar con vectores…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
Matrices de Pauli En la física cuántica, cuando se trabaja con estados propios de spin y operadores para partículas de espín 1/2 en términos de matrices, es posible que vea los operadores SX, Sy, y Sz escrito en términos de Pauli matrices,Teniendo en cuenta que…
La física cuántica y el hamiltoniano Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…